Vectors [9.2]

Many physical quantities--displacement, velocity, force to name a few--have both a magnitude and a direction.
- vector terminology (2-d)
- vectors and scalars
- scalar multiplication of a vector
- vector addition and subtraction
- vector components
- using vectors to define lines
Vectors
A vector is a quantity that has both a magnitude and a direction.
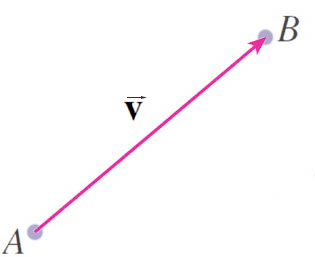 A vector is visually represented by an arrow or a directed line segment which connects two points: the tail (initial point / base) and the head (terminal point / tip).
A vector is visually represented by an arrow or a directed line segment which connects two points: the tail (initial point / base) and the head (terminal point / tip).
- The length of the arrow represents the magnitude of the vector (same as the distance between tail and head) and
- the arrow points in the direction of the vector.
Examples: wind velocity $\myv v$, force $\myv F$, magnetic field $\myv B$, acceleration $\myv a$.
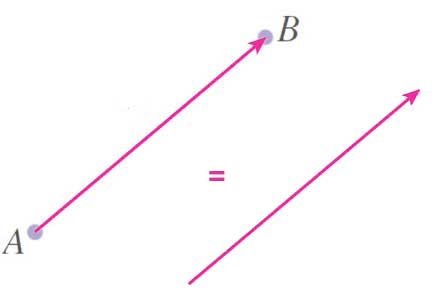
Two vectors are equal if they have the same direction and the same magnitude. (Their positions don't matter.)
Scalar
A scalar number is, for our purposes, usually the same as a real number.
A scalar number can be used to represent a quantity that does *not* have a direction.
For example: time $t$, temperature $T$, the probability that a fish in the ocean is a shark, $p_\text{shark}$.
Notation
Scalar quantities are typically typeset in italics: $$\nonumber t, T, p_{\text shark}$$
Vector quantities are typeset either in bold: \[\nonumber \bf u, \bf v, \bf F \] and/or with an arrow on the top: \[\nonumber \myv u, \myv v, \myv F \]
I encourage you to write an arrow over a letter to distinguish a vector from a scalar, when you're writing mathematics out by hand.
In physics
- "speed", $v$, is a scalar. It can have a value like 30 mph or 6 ft / sec and is always a positive number.
- "Velocity", $\myv v$, is a vector quantity. It might have a magnitude like 4 meters / sec and a direction, such as north-east.
There is a general convention of using the scalar letter to indicate the magnitude (length) of the corresponding vector quantity. For example, acceleration, $\myv a$ has a direction. And its magnitude is $a$: $$a=|\myv a|=\text{the "norm" of }\myv a.$$
Some interchangeable terms for the "length" of a vector:
- magnitude
- norm
- measure
Scalar multiplication
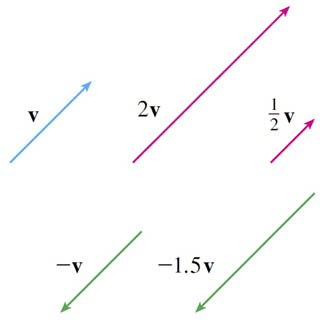
If $c$ is a scalar, and $\myv v$ is a vector, then the scalar multiple $c\myv v$ is the vector with:
- a length of $|c|$ times the length of $\myv v$, and
- a direction which is:
- the same as $\myv v$ if $c \gt 0$, or
- opposite $\myv v$ if $c \lt 0$, or
What relationship (involving scalar multiplication) must exist between two vectors $\myv a$ and $\myv b$ iff [if and only if] they are parallel?
Adding vectors
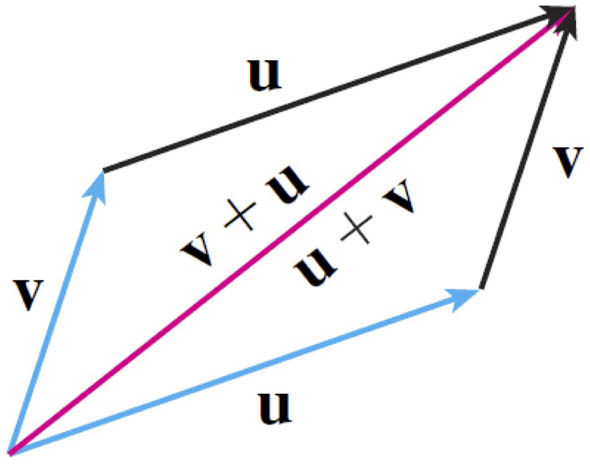
- If $\myv u$ and $\myv v$ are vectors,
- positioned such that the initial point of $\myv v$ is at the terminal point of $\myv u$,
- then the sum $\myv u + \myv v$ is the vector from the initial point of $\myv u$ to the terminal point of $\myv v$.
Vector subtraction
The idea is... \[\nonumber \myv u - \myv v \equiv \myv u + (-1)\myv v \]
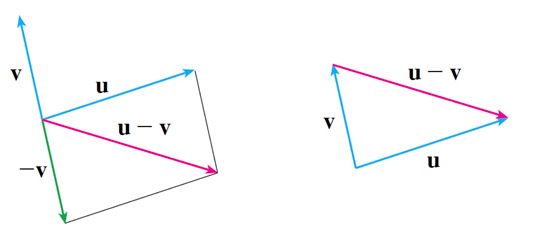
How would you describe $\myv v - \myv u$?

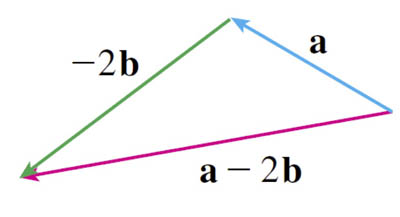
Sketch $\myv a - 2\myv b$
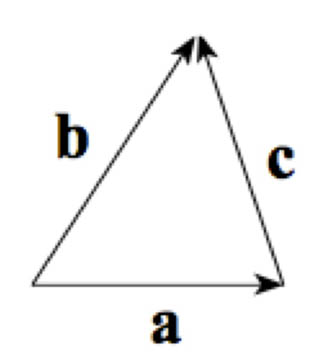 Use vector addition/subtraction to come up with an expression for $\myv c$ in terms of $\myv a$ and $\myv b$.
Use vector addition/subtraction to come up with an expression for $\myv c$ in terms of $\myv a$ and $\myv b$.
Components
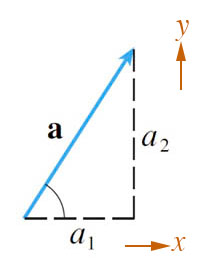 The vector, $\myv a$, is drawn in a 2-d Cartesian coordinate system. The difference between the $x$-coordinate of its tip and of its base is $\Delta x = a_1$. The difference between the $y$-coordinate of its tip and of its base is $a_2$. We write:
$$\myv a=\langle a_1,a_2\rangle$$
where
The vector, $\myv a$, is drawn in a 2-d Cartesian coordinate system. The difference between the $x$-coordinate of its tip and of its base is $\Delta x = a_1$. The difference between the $y$-coordinate of its tip and of its base is $a_2$. We write:
$$\myv a=\langle a_1,a_2\rangle$$
where
- $a_1$ is the "$x$-component" of the vector $\myv a$,
- $a_2$ is the " $y$-component" of $\myv a$.
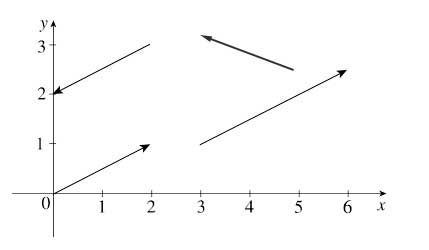
All of these vectors have the same components: $\langle 3,2\rangle$.
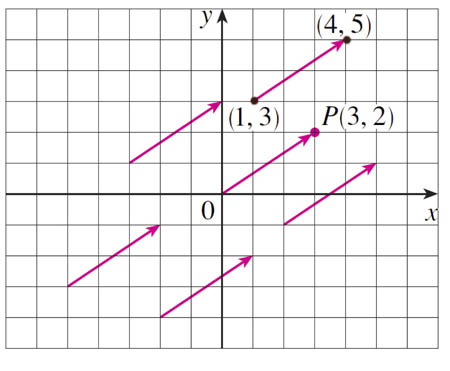
Are all of these vectors equal to each other, or not?
Vector components in 3-d: $$\myv a = \langle a_1,a_2,a_3\rangle \nonumber$$
Length
...of a vector in terms of its components.
Length $|\myv a|$ (a scalar number) of the 2-d vector $\myv a=\langle a_1,a_2 \rangle$: $$|\myv a|=\sqrt{a_1^2+a_2^2}.$$
Length of the 3-d vector $\myv a=\langle a_1,a_2,a_3 \rangle$: $$|\myv a|=\sqrt{a_1^2+a_2^2+a_3^2}.$$
Scalar multiplication (components)
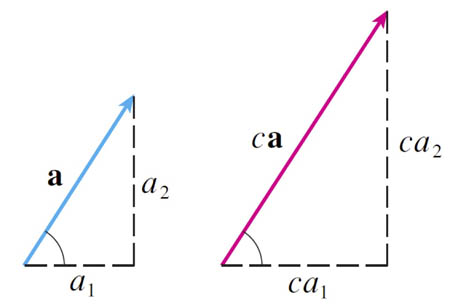
$$c\myv a = \langle ca_1,ca_2 \rangle.$$
Vector addition (and subtraction)
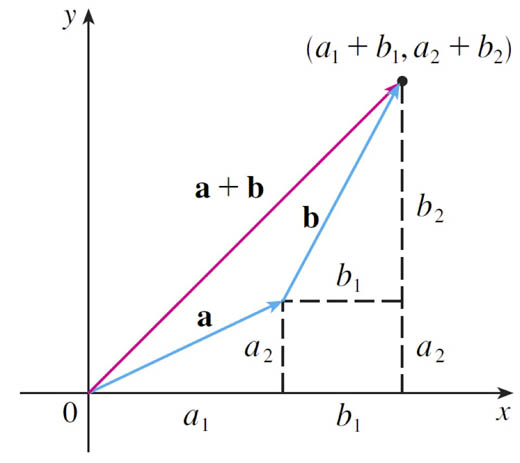
$$ \myv a + \myv b = \langle a_1+b_1, a_2+b_2 \rangle $$
Subtraction: $$ \myv a - \myv b = \langle a_1-b_1, a_2-b_2 \rangle $$
All these results generalize to 3-d.
To Do
- 9.2 Vectors in the plane handout
- Figure out how to specify a line using points, vectors, and any/all of the operations above (scalar multiplication / vector addition / vector subtraction).
- Can you figure out a way of specifying a plane with those same elements?
More properties

Standard basis vectors
The 3 standard "basis vectors" in a Cartesian coordinate system are: $$\myv i \equiv \langle 1,0,0 \rangle; \ \ \myv j \equiv \langle 0,1,0 \rangle; \ \ \myv k \equiv \langle 0,0,1 \rangle$$
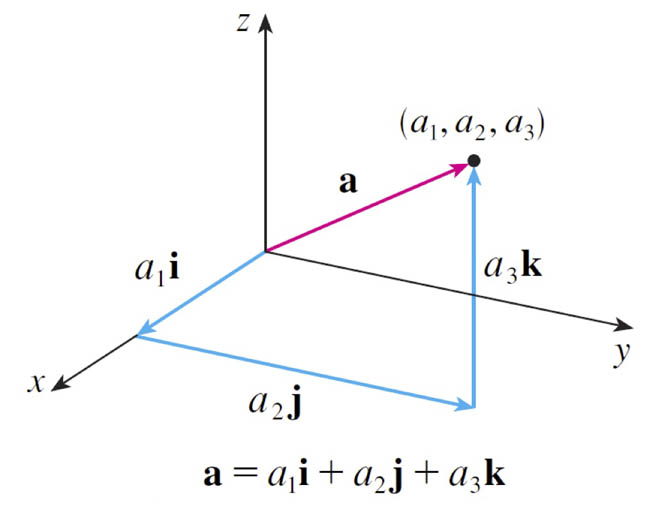
Notice that each of these vectors has a length of 1. That is, they are unit vectors.
A convention that I like, is to indicate unit vectors with the caret symbol up top (instead of an arrow): $$\uv i \equiv \langle 1,0,0 \rangle \equiv \uv x; \ \ \uv j \equiv \langle 0,1,0 \rangle \equiv \uv y; \ \ \uv k \equiv \langle 0,0,1 \rangle\equiv \uv z$$
Find the unit vectors
Find the unit vector...
- that points in the direction $\langle 8, 0, 0 \rangle$.
- that points in the direction $\langle 5,5,0 \rangle$.
- that is opposite to the direction $\langle 1,-1,3 \rangle$.
Using the vectors (not necessarily unit vectors) $\myv b = \langle 1,0\rangle$ and $\myv c = \langle 1,2\rangle$, try to express and $\myv a$ as $r\myv b + s\myv c$.
To do
- Component Vectors
- Lines in the Plane
- Where do they point? Group Work 3
The first lab (that Mathematica notebook on vectors and Mathematica) will be due on Thursday.