Dot product [9.3]

No, no, not that kind of dot product...
There are two ways to form a product of vectors:
- The "dot product" of two vectors, $\myv a \cdot \myv b$ is a scalar.
- The "cross product" of two vectors, $\myv a \times \myv b$ is a vector.
How much energy?

"Work" in physics is the energy expended when a constant force $\myv F$ acts to displace an object by a distance $\myv d$.
Using the convention that $d\equiv |\myv d|$, $F\equiv |\myv F|$, etc...
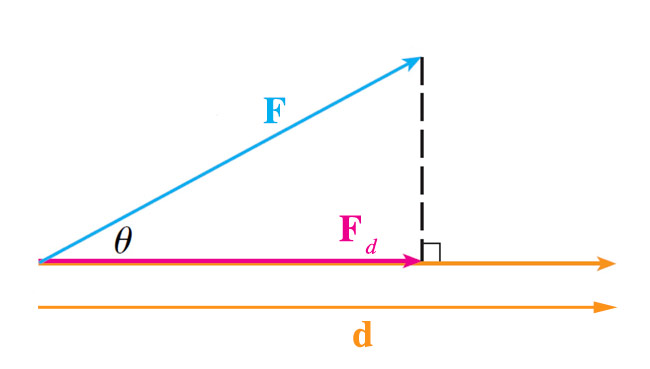
Work is the product of the displacement and the component of the force along the direction of the displacement.
$$\nonumber \text{Work}=F_d d = (F \cos \theta) d$$
We shall see shortly that this can be written as $$\text{Work}=\myv F \cdot \myv d.$$ [Units: Newton-meter = Joule]
So... If the force is at right angles to the displacement no work is done? Can you think of an example?
The dot product
...of two non-zero vectors $\myv a$ and $\myv b$ is defined as $$\myv a \cdot \myv b \equiv |\myv a| |\myv b| \cos \theta$$ where $\theta$ is the smallest possible angle between the vectors when they're drawn with the same initial point. That is, $0 \leq \theta \leq \pi$.
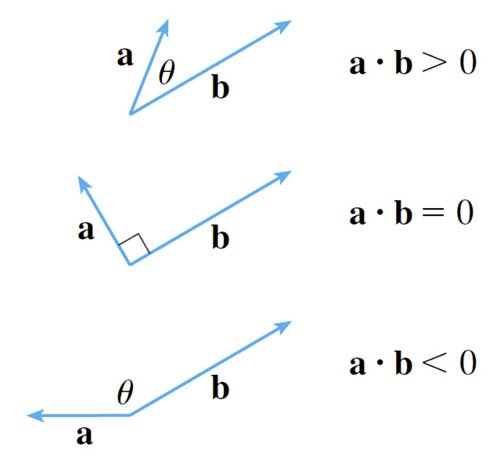
Two vectors are orthogonal (which is a general way of saying "perpendicular") if and only if their dot product is zero. $$\myv a \cdot \myv b=0 \ \ \Leftrightarrow \ \ \myv a \perp \myv b.$$
Component form
The dot product of $\myv a=\langle a_1,a_2,a_3\rangle$ and $\myv b=\langle b_1,b_2,b_3\rangle$ can be written in terms of their components: $$\myv a \cdot \myv b = a_1b_1+a_2b_2+a_3b_3.$$ Examples:
$$\nonumber \langle 2,4 \rangle \cdot \langle 3,-1\rangle = 2(3)+4(-1)=2$$
$$\nonumber \langle -1, 7, 4\rangle \cdot \langle 6,2,\frac 12\rangle = -1(6)+7(2)+4(\frac 12)=10$$
$$\nonumber (\myv i + 2\myv j -3\myv k)\cdot(2\myv j -\myv k)=1(0)+2(2)-3(-1)=7$$
Could also multiply out the product in that last one, and show how orthogonality is used.
Properties of the dot product

Component
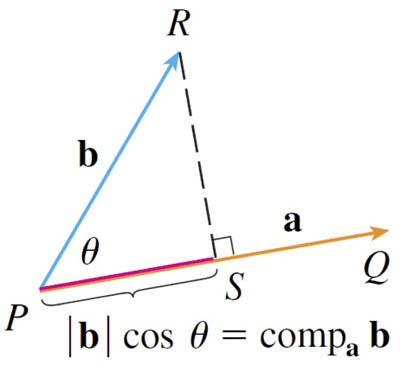
The component of $\myv b$ along $\myv a$ is a scalar: $$\text{comp}_{\myv a}\myv b = b \cos \theta = \frac{|\myv a|}{|\myv a|} |\myv b| \cos \theta = \frac{\myv a \cdot \myv b}{|\myv a|}.$$ ...also called the scalar projection.
Projection
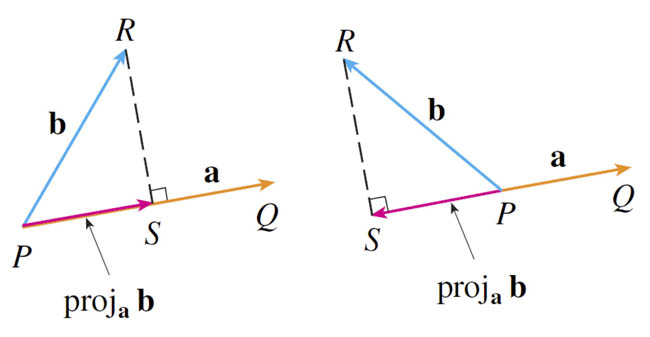
The vector projection of $\myv b$ along $\myv a$ is a vector which points along $\myv a$ and has a length of $b\cos\theta=\text{comp}_{\myv a}\myv b$.
We can construct a vector, $\uv{a}$ of unit length pointing in the $\myv a$ direction like this: $$\uv{a}=\frac{\myv a}{|\myv a|}$$ [I will frequently write $\uv i, \uv j, \uv k$ for the rectangular coordinate unit vectors.]
The vector projection is: $$\text{proj}_{\myv a}\myv b = b\cos\theta \uv a = \frac{\myv a \cdot \myv b}{|\myv a|^2}\myv a.$$
To do
- The Regular Hexagon