Cross product [9.4]
Torque
The torque, $\tau$, necessary to tighten a bolt is related to:
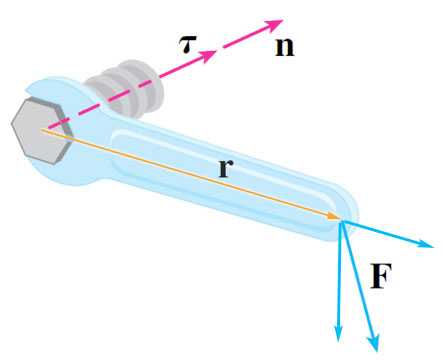
- The force, $F$, exerted on the wrench,
- the distance, $r$, from the axis of the bolt to the point where the force is applied, and
- the relative orientation of $\myv F$ and $\myv r$.
Meaning of the direction of $\myv \tau$? $\myv \tau$ is parallel to the axis of the bolt. $\myv \tau$ points in the direction that a standard, right-hand threaded bolt would advance when tightened.
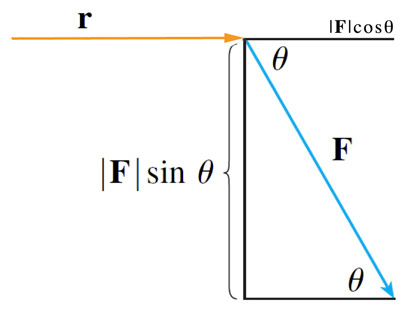Which component of the force--parallel or perpendicular to $\myv r$--is more effective at tightening bolts?
We conclude that $$\tau = rF\sin\theta \nonumber$$ to motivate the...
Definition of the cross product
If $\myv a$ and $\myv b$ are non-zero 3-d vectors, then the cross product $\myv a \times \myv b$ is: $$\myv a \times \myv b \equiv |\myv a| |\myv b| \sin \theta \uv n,$$ where $\theta$ is the smaller angle between $\myv a$ and $\myv b$ ($0\leq\theta\leq \pi$) and $\uv n$ is a unit vector perpendicular to $\myv a$ and $\myv b$ according to the right-hand rule: Curl r.h. fingers from $\myv a$ towards $\myv b$ and your thumb points in the same direction as $\uv n$.
Cross product: order
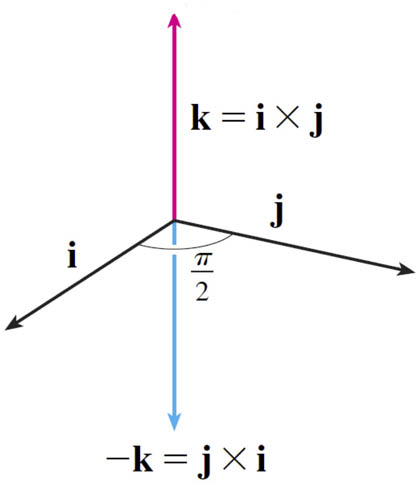With the right-hand rule, the order of the vectors in the cross product matters.
Properties
Geometry
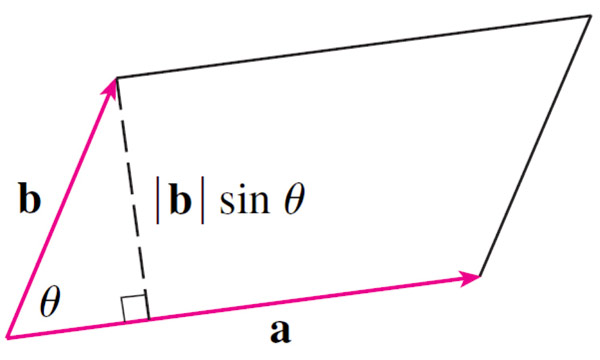
The length of the cross product, $|\myv a \times \myv b|$, is the area of the parallelogram determined by $\myv a$ and $\myv b$.
See www.geogebra.org/m/hjgxmz5a
Computing the cross product
Grinding out the cross product from its components...
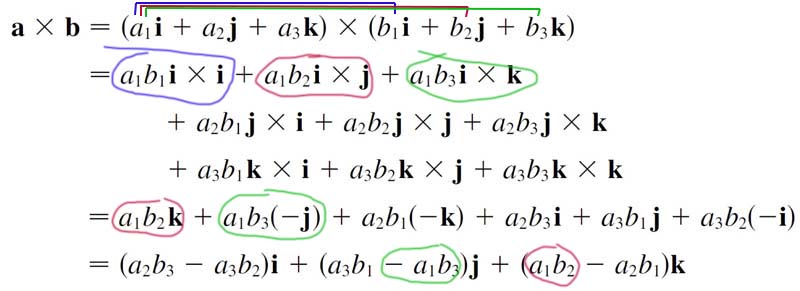
Cross product: determinant method
I remember how to compute the cross product by using the determinant of this 3$\times$3 matrix: $$\myv a \times \myv b = \text{det}\left| \begin{array}{ccc} \uv i & \uv j & \uv k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|.$$
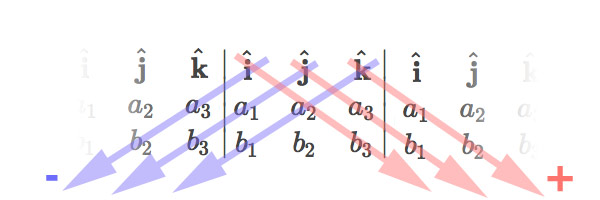
To compute the determinant,
add the red products,
and subtract
the blue products
$$\myv a \times \myv b=(a_2b_3-a_3b_2)\uv i + (a_3b_1-a_1b_3)\uv j+(a_1b_2-a_2b_1)\uv k.\nonumber$$
For example: $\myv a=\langle 1,-2,-4 \rangle$ and $\myv b=\langle 2,4,8\rangle$ $$\begineq \myv a \times \myv b &=& \det\left| \begin{array}{ccc} \uv i&\uv j&\uv k \\ 1 & -2 & -4 \\ 2 & 4 & 8 \end{array} \right|\\ &=&\\ &=&\\ &=& (-2*8 -(-4*4))\uv i+ (-4*2-(1*8))\uv j+ (1*4-(-2*2))\uv k\\ &=& -16\uv j +8\uv k=\langle 0, -16,8\rangle.\nonumber \endeq $$
Triple products
There are many ways to form triple products. Of these, which are vector or scalar quantities?
- $\myv a \cdot (\myv b \cdot \myv c)$
- $\myv a \cdot (\myv b \times \myv c)$
- $\myv a \times (\myv b \cdot \myv c)$
- $\myv a \times (\myv b \times \myv c)$
Scalar triple product
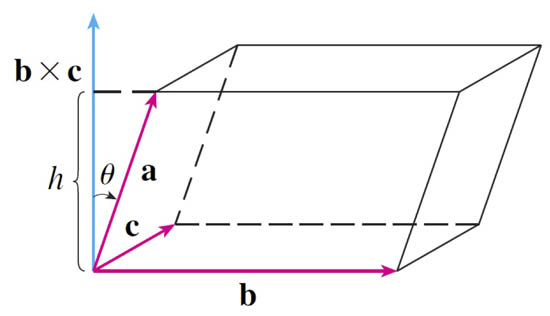
The volume of the parallelipipid determined by $\myv a$, $\myv b$, and $\myv c$ is: $$V= h B$$ Where $B$ is the area of the base (defined by $\myv b$ and $\myv c$) and $h$ is the height of the parallelipid above its base. [Are extremes plausible...?] Now...
- height is $h=|\myv a| \cos\theta$ where $\theta$ is the angle to the vector direction which is perpendicular to the base.
- area of the base is $B=|\myv b \times \myv c|$.
...and $\myv b \times \myv c$ is a vector perpendicular to the base, as shown, with the magnitude of $B$.
So, the volume can be written as $$V=|\myv a|\cos\theta |\myv b \times \myv c| = \myv a \cdot (\myv b \times \myv c).$$
[Without proof] This may also be calculated from: $$\myv a \cdot (\myv b \times \myv c) = \text{det}\left| \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right|$$
Vector triple product
$$\myv a \times (\myv b \times \myv c) =(\myv a \cdot \myv c)\myv b -(\myv a \cdot \myv b)\myv c.$$
Perpendicular to $\myv a$
Consider the set of all vectors $\myv b$ and $\myv c$ such that $\myv b \times \myv c = k \myv a$. (a scalar multiple of $\myv a$). What geometrical entity do these vectors form?
To do
- Messing around with the cross product.