Lines and planes [9.5]

Casa Batlló by Antoni "enemy of the straight line" Gaudí and Josep Maria Jujol.

Line segment

You know that "two points determine a line".

In 3-d we should be able to construct a line given:
    2 points $\times$ 3 coordinates / pt = 6 numbers.

In yesterday's class, you figured out (in two dimensions) that this equation specifies all the points on the line segment between $P$ and $Q$

$$(\,x(t), y(t)\ )= (P_x,P_y) +t( \myv{PQ}_x, \myv{PQ}_y )\ :\ 0\lt t \lt 1.$$ You figured out that if we lifted the restriction $0\lt t \lt 1$, and allowed $t$ to be any real number, positive or negative, that we'd have the equation of the line that runs through both $P$ and $Q$!

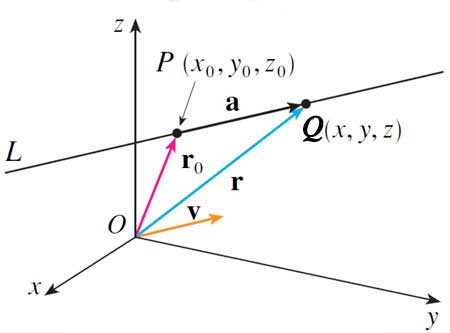
Translating this into the terms of the diagram above (and generalizing to 3 dimensions...)

• $\myv r_0$ is the position vector with tail at the origin, and head at point $P$.
• $\myv{PQ}\equiv \myv a$ is the difference vector, which runs from $P$ to some other point $Q$
• Let's say that $\myv v$ is some other vector, that is parallel to $\myv a$. Any vector parallel to $\myv v$ can be expressed as some scalar multiple $t\myv v$ of $v$.

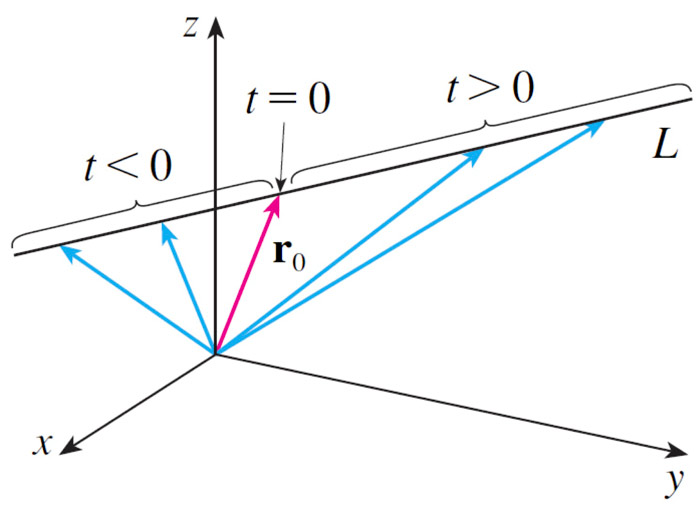
So, using vector addition, we can express the set of points on the line in parametric form as: $$\myv r(t)=\myv r_0 + t\myv v.$$

Tip: WebAssign problem 9.5.002 In part 1 of this question, they ask you for the "vector equation of a line". They're expecting $$r_0+tv$$ with no special vector formatting. To get the subscript, type 'r_0`. When you type the underscore character, '_', you won't see it appear, but when you type the 0, it should show up as a subscript.

...And since $\myv r_0$ and $\myv v$ each have three components, once again, we have the 6 scalars needed to uniquely specify a line, only packaged up this time as the coordinates of a point and the components of a vector.

In component form

$$\begineq \myv r(t) &=& \myv r_0 + t\myv v = \langle x_0,y_0,z_0\rangle+t\langle a,b,c\rangle \\ &=& \langle x_0+ta, y_0+tb, z_0+tc \rangle .\endeq $$ or $$x(t)=x_0 +at;\ \ y(t)=y_0 +bt;\ \ z(t)=z_0 +ct$$

Each of these can be solved for $t$, and then setting each form of $t$ to the others: $$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}.$$

These are the symmetric equations. Notice that $a$, $b$, $c$ are the components of $\myv v$, a vector parallel to the line $L$.

Example

Consider two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

Do they intersect?

Solution: If they intersect at some common point (x,y,z), then that point should be a simultaneous solution in $s$ and $t$ to these three equations: $$1+t=2s;\ \ -2+3t=3+s;\ \ 4-t=-3+4s$$

Those same two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

Are the lines parallel?

Solution: Re-arrange the equations into the form of the symmetric equations (solve each equation for $t$...or for $s$...) to find the components (denominators) of a vector parallel to each line.

Lines which are not parallel to each other, and do not intersect are called skew lines.

To do

• Lines in the plane

Planes

A plane can be determined by

• a point $P_0$ in the plane and
• a normal vector, $\myv n$, which is orthogonal (normal) to the plane.

In pictures...

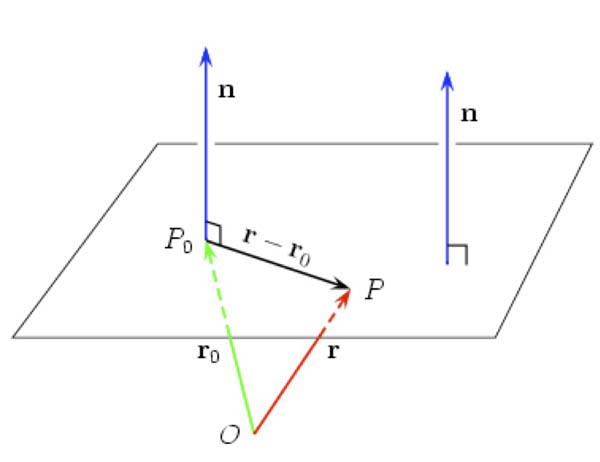
• $\myv r_0=\langle x_0, y_0, z_0 \rangle$ is a vector pointing at $P_0$.
• $\myv n = \langle a, b, c \rangle$ is the normal vector.
• $\myv r=\langle x,y,z\rangle$: Some point in the plane, which must satisfy the condition that $\myv r -\myv r_0$ is perpendicular to $\myv n$:

  $$\begineq 0&=&\myv n \cdot (\myv r-\myv r_0)\\ &=&\langle a,b,c \rangle \cdot \langle x-x_0,y-y_0,z-z_0\rangle\\ 0&=&a(x-x_0)+b(y-y_0)+c(z-z_0)\rangle\\ \endeq $$

Pushing the equation above one step further, let's expand the products and add up all the constant terms calling their sum $k$: $$\begineq ax_0+by_0+cz_0&=&ax+by+cz\\ k&=&ax+by+cz \endeq $$

So that if you see an equation for a plane such as: $$56=7x-3y+2z,$$ You can just read off the components of a normal vector to the plane as: $$\myv n=\langle 7,-3,2 \rangle.$$

Example

Example four from book, but using a cross product to find the surface normal...

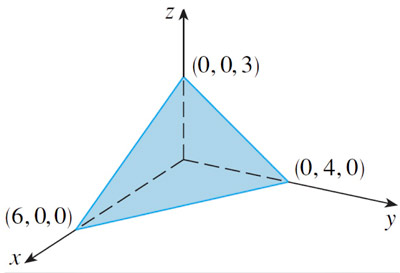
First find the normal to the plane.
[Find two vectors that are in the plane, and then take their cross product.]

Then find the equation for the plane. [Take as $\myv r_0$ any of the three points shown.]

Find the surface normal:
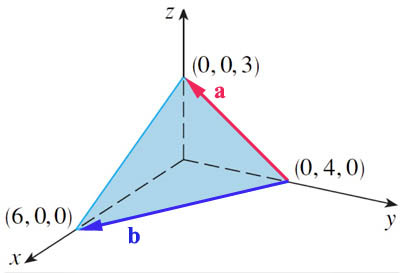$\myv a=\langle 0,-4,3 \rangle$
$\myv b=\langle 6,-4,0 \rangle$
$\myv a \times \myv b=12\uv i+18\uv j+24\uv k$

Let's take for the normal vector... $$\myv n=2\uv i+3\uv j+4\uv k =a \uv i + b \uv j +c \uv k$$

Picking $(0,4,0)$ as the point in the plane, then the prescription above is... $$\begineq 0 &=&a(x-x_0)+b(y-y_0)+c(z-z_0)\\ &=&2(x)+3(y-4)+4(z) = 2x+3y-12+4z\\ \endeq$$ So, the equation for the plane can be written as: $$2x+3y+4z = 12.$$ where a normal vector to the plane was $\myv n=\myc{2,3,4}$.

Notice that when the equation for a plane is written in this form that you can read off the components of the normal vector from the coefficients of $x$, $y$, and $z$!

Image credits

vgm8383