Derivatives and integrals of vector functions [10.2]
Derivatives
$$\frac{d\myv r}{dt} \equiv \myv r'(t) = \lim_{h\to 0} \frac{\myv r(t+h)-\myv r(t)}{h}.$$
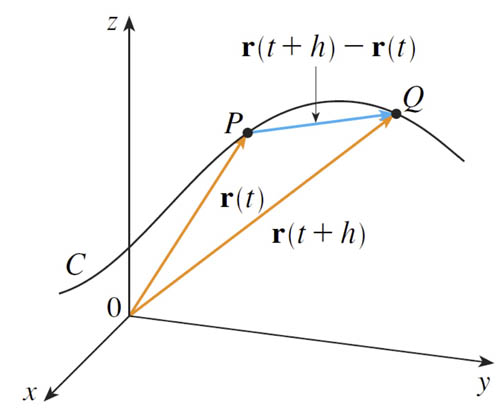
In the limit $h \to 0$, $\myv r'(t)$ is a vector which is tangent to the curve at $\myv r(t)$.
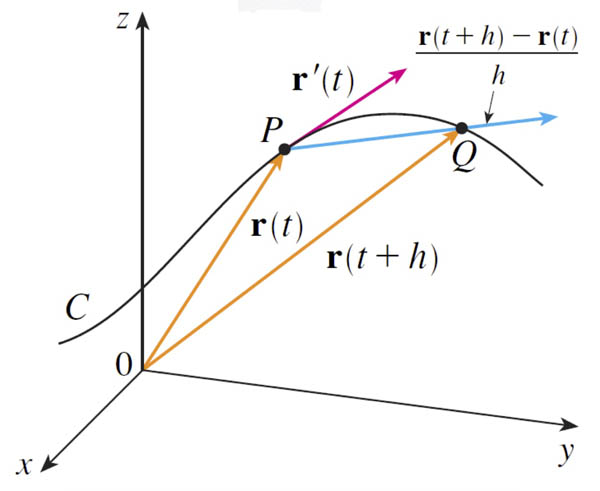
Mess around with 10.2.deriv.nb to see these relationships.
Differentiation - components
A theorem: if $\myv r(t)=\langle f(t),g(t),h(t)\rangle = f(t)\uv i+g(t)\uv j+h(t) \uv k$, where $f$, $g$, and $h$ are differentiable functions, then $$\myv r'(t)=\langle f'(t),g'(t),h'(t)\rangle = f'(t)\uv i+g'(t)\uv j+ h'(t)\uv k.$$
Differentiation rules
Cusp?
A vector function $\myv r(t)=\myc{f(t),g(t),h(t)}$ might have a cusp if $\myv r'(t)=0$.
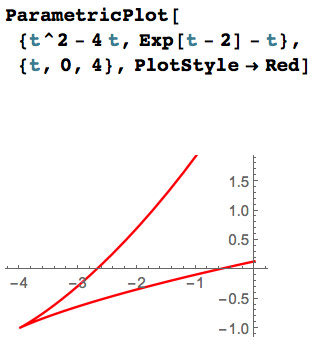At right: $\myv r(t)=\myc{t^2-4t,e^{t-2}-t}$, so
$\myv r'(t)=\myc{2t-4,e^{t-2}-1}$.
And... $\myv r'(2)=\myc{0,0}$.
More on tangent vectors
The line tangent to the curve at $\myv r(t_0)$ is: $$\myv L(t) = \myv r(t_0) + t \myv r'(t_0).$$
The unit tangent vector is given by: $$\uv T(t) = \frac{\myv r'(t)}{|\myv r'(t)|}.$$
Theorem: If a vector function, $\myv r(t)$, has constant length, then its derivative, $\myv r'(t)$, is perpendicular to $\myv r(t)$.
Proof:
- We're assuming that the length of $|\myv r(t)|$ is not changing. That is, $$\frac{d}{dt}|\myv r(t)|=0.$$
- Then, the length${}^2$ is also unchanging: $$\begineq 0&=&\frac{d}{dt}|\myv r(t)|^2\\ &=&\frac{d}{dt}(\myv r\cdot\myv r)=\myv r'\cdot \myv r+\myv r\cdot\myv r'\\ 0 &=&2\myv r'\cdot \myv r\\ \endeq $$
- Therefore $\myv r' \perp \myv r$.
Example: $\myv r(t)=\langle cos(t),sin(t)\rangle$. Taking the derivative of its component functions... $$\nonumber \myv r'(t)=\langle -\sin(t),\cos(t)\rangle.$$ [See tangent.nb]
The unit tangent
- The Unit Tangent $\uv T(t)=\frac{\myv r'(t)}{|\myv r'(t)|}$ has constant length 1.
- The only characteristic of $\uv T(t)$ that changes as $t$ changes is its direction.
- $|d\uv T/dt|$ measures the rate of change of the direction of the unit tangent vector. ["units" are radians per $t$-unit].
Example: $\myv r(t)=\langle t^3,t^6\rangle$
Integrals
$$\begineq \int_a^b \myv r(t)\,dt &=& \int_a^b \langle f(t),g(t),h(t)\rangle\,dt\\ &=& \(\int_a^b f(t)\,dt\)\uv i + \(\int_a^b g(t)\,dt\)\uv j + \(\int_a^b h(t)\,dt\)\uv k \endeq $$
These are the components of $\myv R(t)$, the anti-derivative of $\myv r(t)$: $$\int_a^b \myv r(t)\,dt = \left. \myv R(t)\right|_a^b = \myv R(b)-\myv R(a). $$ And $\myv R'(t)=\myv r(t)$.
To do
10.2 - the grim reaper