Which way to go?
The hiking question(s)
Which direction should I go...
- to go up most steeply?
- to go down most steeply?
- to keep moving around the mountain while staying at the same altitude?
- Also, how steep is the path I'm on right now?
Ummmmm... Actually our brains working with our eyes are pretty good at answering such questions unconsciously with little or not calculus training!
We will instead be trying to answer questions about surfaces for which we have a mathematical description (often a function). The surfaces will mostly be continuous and well behaved.
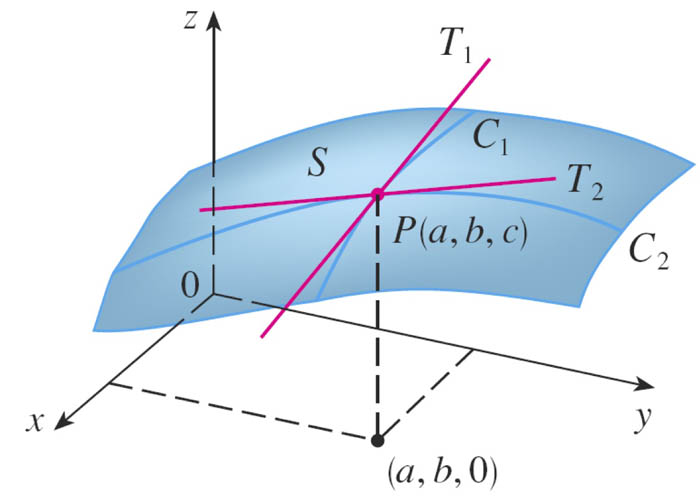
The slope...in any direction
For a function, $f(x)$, of one variable, $\frac{df}{dx}$ is *the* slope of the graph at $x$.
But on a mountain (=surface), slope depends on the direction of motion. Or we could say, it depends on the path taken.
Partial derivatives [11.3]
If $f$ is a function of two variables, then its partial derivatives are the functions $f_x$ and $f_y$ defined by $$f_x(x,y)=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}$$ $$f_y(x,y)=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}{h}$$ In the first definition, $y$ is constant and $x$ varies. In the second one $x$ is constant and $y$ varies.
Notation... $$f_x(x,y)\equiv f_x\equiv \frac{\del f}{\del x}\equiv \frac{\del}{\del x}f(x,y)\equiv \frac{\del z}{\del x}\equiv D_x f.$$ $$f_y(x,y)\equiv f_y\equiv \frac{\del f}{\del y}\equiv \frac{\del}{\del y}f(x,y)\equiv \frac{\del z}{\del y}\equiv D_y f.$$ with $z=f(x,y)$.
[I have seen $f_1$ or $D_1$ very rarely].
Rules for calculating partial derivatives
- To find $f_x$, regard $y$ as constant, and differentiate $f(x,y)$ with respect to $x$.
- To find $f_y$, regard $x$ as constant, and differentiate $f(x,y)$ with respect to $y$.
For example: $$f(x,y)=3xy^2$$
$$f_x=\frac{\del }{\del x} (3y^2)x=3y^2$$
$$f_y=\frac{\del }{\del y}(3x)y^2=(3x)*2y=6xy$$
In CoCalc (at right):
Mathematica: D[f,x], D[f,y]
Visualizing
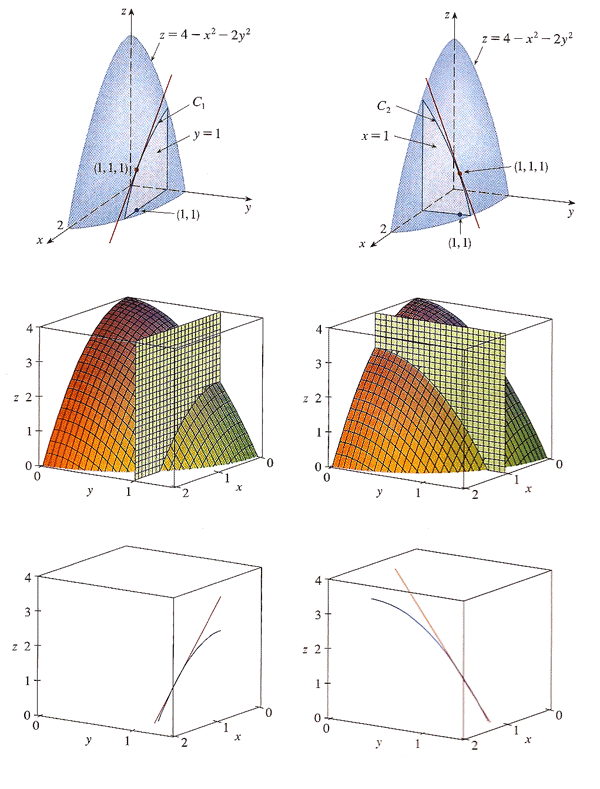
To do
- Tabular data - Just 1-3.
- Graphical data - Just 1-3.
Higher order derivatives
$$(f_x)_x=f_{xx}=\frac{\del}{\del x}\left( \frac{\del f}{\del x}\right)=\frac{\del^2 f}{\del x^2} =\frac{\del^2 z}{\del x^2}.$$ $$(f_x)_y=f_{xy}=\frac{\del}{\del y}\left( \frac{\del f}{\del x}\right)=\frac{\del^2 f}{\del y \del x} =\frac{\del^2 z}{\del y \del x}.$$ $$(f_y)_x=f_{yx}=\frac{\del}{\del x}\left( \frac{\del f}{\del y}\right)=\frac{\del^2 f}{\del x \del y} =\frac{\del^2 z}{\del x \del y}.$$ $$f_{yy}=(f_y)_y=\frac{\del}{\del y}\left( \frac{\del f}{\del y}\right)=\frac{\del^2 f}{\del y^2} =\frac{\del^2 z}{\del y^2}.$$
Interpretation
$f_x$ means...what?
$f_{yy}$ means...what? It is the curvature or concavity of the curve of a path in the $y$ direction--along the lines of the second derivative of a function of one variable.
$f_{yx}$ is the rate of change of the slope in the $y$ direction, as you increase $x$. But is there a word like "concavity" or "slope" to describe what that means graphically? See this visualization of $f_{yx}$
Example
Consider... $$f (x, y) = x^3 + x^2y^3 – 2y^2$$
$$f_x=3x^2+2xy^3;\ \ \ f_y=3y^2x^2-4y$$
$$f_{xy}=\frac{\del f_x}{\del y}=6xy^2;\ \ \ f_{yx}=\frac{\del f_y}{\del x}=6xy^2$$
$$f_{xx}=\frac{\del f_x}{\del x}=6x+2y^3;\ \ \ f_{yy}=\frac{\del f_y}{\del y}=6yx^2-4$$
Clairaut's theorem
Suppose $f$ is defined on a disk $D$ that contains the point $(a,b)$. If the functions $f_{xy}$ and $f_{yx}$ are both continuous on $D$, then $$f_{xy}(a,b)=f_{yx}(a,b).$$
Another way of saying this is $$\frac{\del}{\del y}\left(\frac{\del f}{\del x}\right) =\frac{\del}{\del x}\left(\frac{\del f}{\del y}\right).$$
See Clairaut's theorem and the meaning of $f_{xy}$.
Differentiability
If $z=f(x,y)$, then $f$ is differentiable at $(a,b)$ if $\Delta z$ can be expressed in the form $$\Delta z = f_x(a,b) \Delta x + f_y(a,b) \Delta y + \epsilon_1 \Delta x +\epsilon_2 \Delta y$$ where $\epsilon_1\to 0$ and $\epsilon_2 \to 0$ as $(\Delta x, \Delta y)\to 0$.
In hiking terms
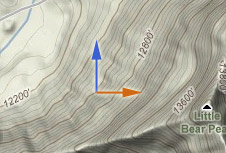How does your altitude change ($\Delta z$)?
Well, it depends on how far east ($\Delta x$) and north ($\Delta y$) you move,
...and also on the the east-west slope ($f_x$) and the north-south slope. It's a pretty good approximation to say that your height will change by...
$$\label{hikeit} \Delta z \approx f_x \Delta x + f_y \Delta y.$$
This is, in principle, the resolution to at least one of the hiking questions:
- If you choose to step in an arbitrary direction, as specified by $\Delta x$ and $\Delta y$,
- Then, knowing only two local characteristics of the surface, $f_x$ and $f_y$,
- You can approximate your change in height.
Theorem: If the partial derivatives $f_x$ and $f_y$ exist near $(a,b)$, and if they are continuous at $(a,b)$, then $f$ is differentiable at $(a,b)$.
In hiking terms: The approach of using Eq (\ref{hikeit}) to calculate your change in height won't work on top of a sharp ridge, or at the edge of a cliff.
To Do
- Mixed partials