Linear approximations

The board is tangent to the bowling ball at the point of contact.
Tangent planes
Suppose $f$ has continuous partial derivaties. An equation of the tangent plane to the surface $z=f(x,y)$ at the point $P(x_0,y_0, z_0)$ is $$z-z_0=f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$$
Linear approximation
$$z = f(a, b) + f_x(a, b)(x – a) + f_y(a, b)(y – b)$$ is called the linear approximation or the tangent plane approximation of $f$ at $(a, b)$.
The differential of $f$ is $$dz \equiv f_x(x,y)\,dx+f_y(x,y)\,dy = \frac{\del f}{\del x}dx+ \frac{\del f}{\del y}dy.$$
In the limit of very small 'steps', $dx$ and $dy$, the linear approximation can be written as $$f(x,y)=f(a,b)+dz.$$
Geometric view
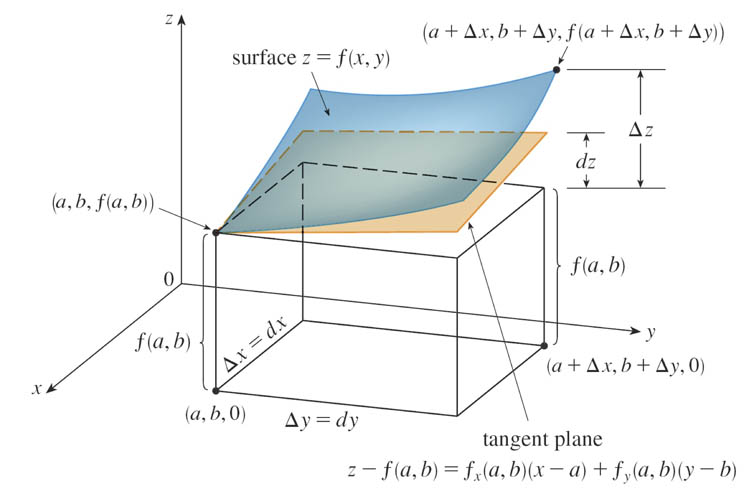
Hiking view
The hiking approximation $$\label{hikeit} \Delta z \approx f_x \Delta x + f_y \Delta y$$
- becomes exact as your stepsize becomes small, and
- is apparently equivalent to the linear approximation, and
- only works if there's a unique plane tangent to the surface.
To Do
- Finish Tabular data
- Finish Graphical data