Maximum and Minimum Values
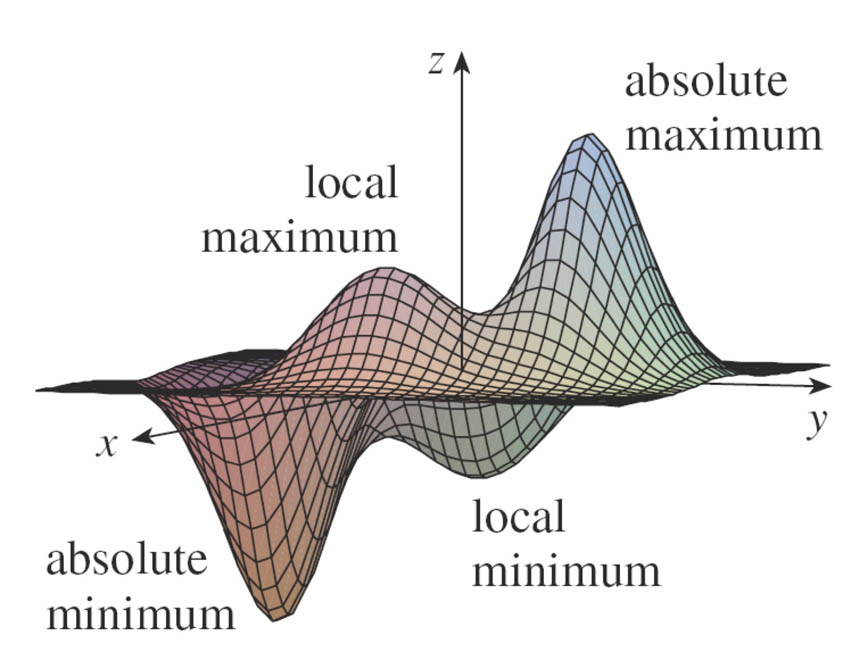
A definition and a theorem
A function of two variables has a local maximum at $(a,b)$...
- if $f(x,y)\leq f(a,b)$ when $(x,y)$ is near $(a,b)$.
- [This means that $f(x,y)\leq f(a,b)$ for all points $(x,y)$ on some disk centered at $(a,b)$.]
- The number $f(a,b)$ is called the local maximum value
...if instead $f(x,y)\geq f(a,b)$ near $(a,b)$, then $f(a,b)$ is a local minimum value.
Theorem if $f$ has a local maximum (or minimum) at $(a,b)$, and the first order partial derivatives exist there, then $$f_x(a,b)=0 \ \ \text{ and }\ \ f_y(a,b)=0.$$
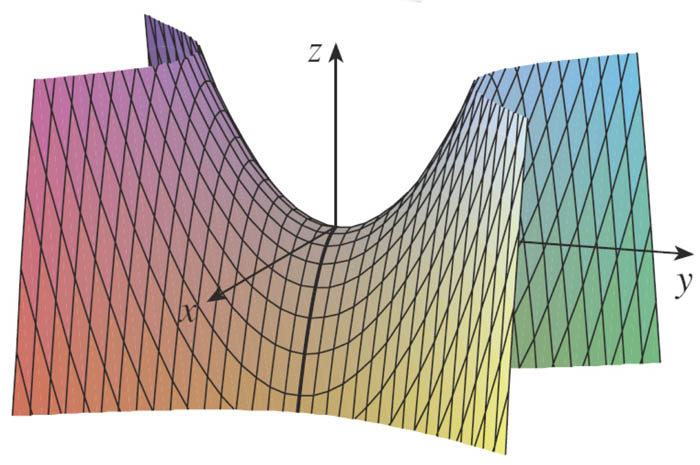
Does this relationship go the other way?
Consider the saddle point pictured...
Second derivatives test
In calculus of one variable, the second derivative can be used to decide if a point is a maximum, minimum, or neither. There's a second derivatives test for functions of two variables:
Suppose that the first partial derivatives exist, and vanish at $(a,b)$, that is $f_x(a,b)=f_y(a,b)=0$, then $(a,b)$ is a critical point.
Now, suppose that in addition, the second partial derivatives of $f$ also exist on a disk centered at $(a,b)$. The determinant of the Hessian matrix of 2nd derivatives, $D$, turns out to be useful for testing critical points: $$\begineq D(a,b)&\equiv& f_{xx}(a,b)f_{yy}(a,b)-\[f_{xy}(a,b)\]^2\\ &=&\text{det} \begincv f_{xx} & f_{xy}\\ f_{yx} & f_{yy} \endcv \endeq $$
Second derivatives test
If $(a,b)$ is a critical point of $f$, then....
- if $D \gt 0$ and $f_{xx} \gt 0$, $\Rightarrow f(a,b)$ is a local minimum.
- if $D \gt 0$ and $f_{xx} \lt 0$, $\Rightarrow f(a,b)$ is a local maximum.
- if $D \lt 0$ then f(a,b) is a neither a local maximum, nor a local minimum. (saddlepoint)
If $D=0$ the test is inconclusive. The critical point might be a max, a min, or a s.p.
Problem
Find three positive numbers whose sum is $n$, and whose product is a maximum.
We could define these two conditions as: $$x+y+z=n$$ and $$xyz=\text{maximum}.$$
One approach (outlined in the tutorial) is
- Solve the first equation for $z$: $$z=n-x-y$$
- Define the product of the three numbers as a function of $x$ and $y$, by subbing in for $z$: $$f(x,y)=xy(n-x-y)=nxy-x^2y-xy^2.$$
- The maximum of this function will occur when both $\frac{\del f}{\del x}=0$, and $\frac{\del f}{\del y}=0$.
- This is two equations and there are two unknowns, $x$ and $y$. Solve the two equations for $x$ and $y$.
- Actually there is more than one $(x,y)$ pair that solves this, but you can try them out, and see which gives the largest product. (Hint, some of them involve $x=0$ or $y=0$, which will give a minimum for the product, instead of a maximum).