Area between curves
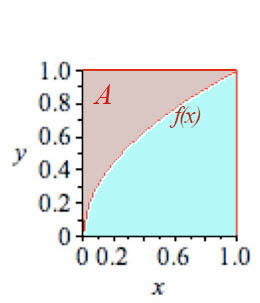How to calculate the
area in red above the function $f(x)=\sqrt x$?
Many ways!...
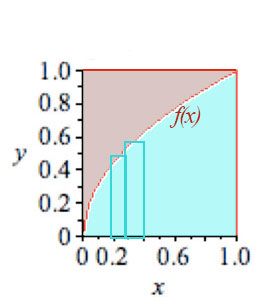A single integral over $x$
The area of the box is $1 \times 1=1$. Calculate the area below $f(x)$ with an integral, and subtract from 1:
$$\begineq \int_{x=0}^1 \sqrt x\,dx&=&\int_0^1 x^{\frac 12}\,dx\\ &=&\left. \frac{x^{\frac 32}}{3/2}\right|_0^1 = \frac 23 (1-0)=\frac 23. \endeq $$ So our desired area is $$A=1-2/3=1/3.$$
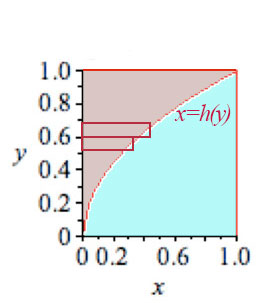A single integral over $y$
If $f(x)=y=\sqrt x$, then with a little algebra we can invert the function: $$\begineq y&=&\sqrt x\\ y^2&=&(\sqrt x)^2\\ y^2&=&x \\ \endeq$$
Express the red curve as the function $x=h(y)=y^2$ and integrate over $y$:
$$ \int_{y=0}^1 y^2\,dy=\left. y^3/3\right|_0^1=1/3-0=1/3.$$ Ah, the same answer.
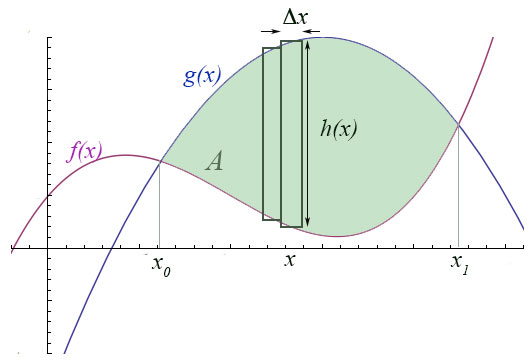
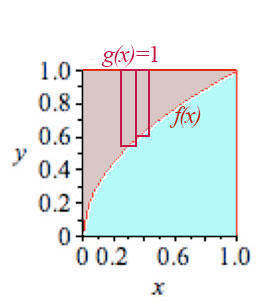Area between curves
An integral over $x$ is the Rieman sum of rectangles of a height which varies with $x$. That rectangle "height" could instead be given by the difference between the two functions shown
$$\begineq
\int_{x=0}^1 (g(x)-f(x))\,dx&=&\int_{x=0}^1(1-\sqrt{x})=\int_0^1 dx -\int_0^1\sqrt x\,dx\\
&=&\left. x\right|_0^1-2/3=1-2/3=1/3.
\endeq
$$
To Do - Area Between Curves
- In Lab 06, Exercise 1, You'll plot the curves $f(x)=\ln[x]$ and $g(x)=(x-1)^2$ and find the area between the points of intersection of the functions.
- In Exercise 2, you'll use parametric plotting to plot $x=y^2$ and $x=1-y$.
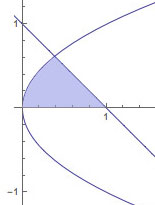Find the area of the region shown, between the two curves and above the $x$-axis. Do this, by using $y$ as your integration
variable (instead of $x$).
Integral of 1 as width of interval
This integral:
$$\int_a^b 1 \,dx= \int_a^b \color{gray}{1 \,}dx= \int_a^b \color{lightgray}{1 \,}dx=
\left. x\right|_a^b=b-a$$
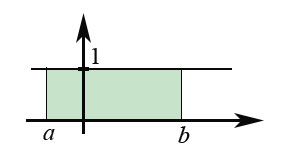is a very contorted way of writing the width of the interval from $a$ to $b$.
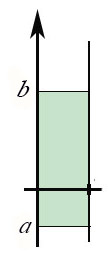Or, turning the picture by 90 degrees, the vertical distance from $a$ to $b$ is
$$\int_a^b \color{lightgray}{1\,}dy=b-a.$$
In the picture of the area between two curves, we could write the height $h(x)=g(x)-f(x)$ of the rectangle at $x$ as
$$h(x)=\int_{y=f(x)}^{g(x)}dy.$$
Then, the area, $A$, between the curves is $$\begineq A&=&\int_{x_0}^{x_1}h(x)\,dx=\int_{x_0}^{x_1}\left(\int_{y=f(x)}^{g(x)}dy\right)\,dx\\ &=&\int_{x_0}^{x_1}\int_{f(x)}^{g(x)}dy\,dx\equiv \iint_A dA \endeq$$ where $dA=dx\,dy$ is a small chunk of area, integrated over the region, $A$, shown.
Original problem as a double integral
So, back to our original problem, which can be written in a new way. We evaluate the integrals from the inside out...
$$\begineq A
&=& \iint_A dA=\int_{x=0}^{1} \int_{y=\sqrt x}^1 dy\,dx \\
&=&\int_{x=0}^{x=1} \left(\int_{y=\sqrt x}^1 1\,dy\right)\,dx
=\int_{x=0}^{x=1} \left(\left. y\right|_{y=\sqrt x}^1\right)\,dx\\
&=&\int_{x=0}^{x=1} \left(1-\sqrt x\right)\,dx = 1/3.
\endeq
$$
To do
Do Exercise 3 in Lab 06, in which you'll convert the integral of Exercise 1 to a double integral over $dA=dy\,dx$.
Then...
- Double Integrals and Areas: Write out each area as a double integral. You do not need to evaluate the integrals. For each area, you should be able to write the area as one double integral. (Hint: You may need to think about integrating $x(y)\,dy$ instead of $y(x)\,dx$.)