Iterated integrals & partial integration

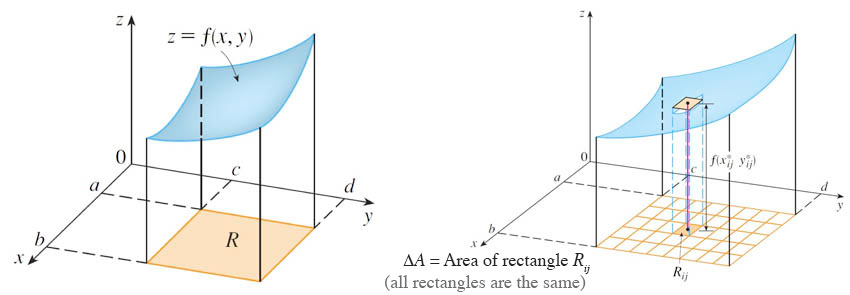
We saw that the double integral: $$\iint_R f(x,y)\,dA$$ represents the volume between the rectangle $R\equiv[a,b]\times[c,d]$ (in the $x,y$ plane) and the surface $z=f(x,y)$ above $R$.

Now we'll see how to evaluate such an integral.

Partial Integration

How to evaluate a double integral like $$\iint_R f(x,y)\,dA=\iint_R f(x,y)\,dx\,dy?$$

We define partial integration of a function $f(x,y)$ with respect to $y$ with this notation: $$\int_{y=c}^d f(x,y)\,dy=A(x).$$ A(x) is the result of

• Treating $x$ as a constant,
• carrying out the integration with respect to $y$.

example: $$\begineq\int_0^1 (2-x-y)\,dy&=&\int_0^1 (2-x)\,dy-\int_0^1 y\,dy\\ &=&(2-x)\int_0^1 dy-\int_0^1 y\,dy\\ &=&(2-x)\,\left. y \right|_0^1-\left.\frac12 y^2\right|_0^1\\ &=&(2-x)(1-0)-\frac12(1^2-0^2)\\ A(x)&=&2-x-\frac12=\frac32-x. \endeq $$

We write it as $A(x)$ because it is the area resulting from the partial integration w.r.t. $y$, but typically the result is a function of $x$.

Double integral

The double integral is the result, next, of carrying out the integration of $A(x)$ with respect to $x$: $$\begineq \iint f(x,y) dA&=&\int_{x=a}^b A(x)\,dx\\ &=&\int_{x=a}^b \left(\int_{y=c}^d f(x,y)\,dy \right)\,dx\\ &=&\int_{x=a}^b \int_{y=c}^d f(x,y)\,dy \,dx\\ \endeq $$

This rather sloppy way of writing the double integral leaves it unclear whether you should evaluate the partial integral of $y$ first, and then integrate over $x$, or vice versa. Perhaps it doesn't matter?

Fubini's Theorem

...says that for a rectangular region $R$ and some pretty general assumptions, the order of partial integration does not matter.

Example 1

Find the volume underneath $f(x,y)=2-x-y$ and above the rectangle defined by points in the $x$-$y$-plane: $0\lt x \lt 1$, and $0\lt y\lt 1$. (Alternately, $R=[0,1]\times[0,1]$.)

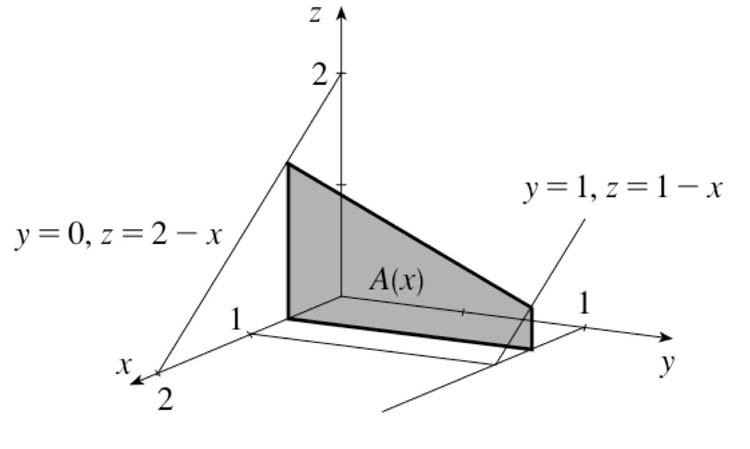
$$ \begineq V= \iint (2-x-y)\,dA &=& \int_{x=0}^1\int_{y=0}^1(2-x-y) dy dx \\&=& \int_{x=0}^1\left(\int_{y=0}^1 (2-x-y)\,dy\right) dx \endeq$$

We already carried out the partial integral in $(...)$. Substituting the result back into the expression for $V$, $$ \begineq V&=&\int_{x=0}^1\left(\frac 32 - x\right)\,dx = \frac 32\int_0^1 dx -\int_0^1x\,dx\\ &=&\frac32-\frac12=1 \endeq $$

Example 2

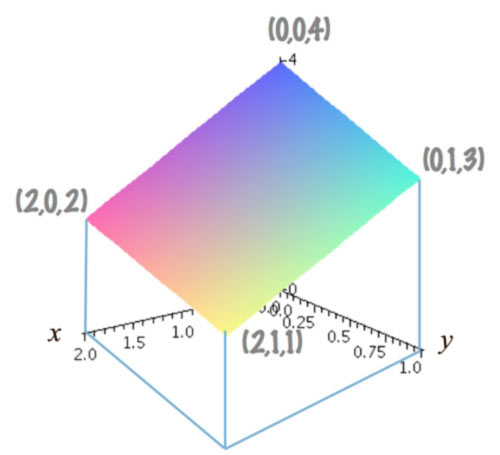
The function for the surface is $f(x,y)=4-x-y$.

• Estimate the volume under this surface, for example, by estimating the average height of the surface, then multiplying by the area of the rectangle $R$ underneath.
• Evaluate the double integral to find the exact volume.

How to do this in CoCalc:

How to do this in Mathematica.

To Do

• Double integrals - practice: #1-4
• The shape of the solid