Scalar Line Integrals

Line integral (scalar)

Area of the wandering, irregular fence...

Consider the smooth curve, $C$, in the $x$-,$y$-plane described by the vector function parameterized in terms of $t$ $$\myv r(t)=\langle x(t),y(t)\rangle.$$
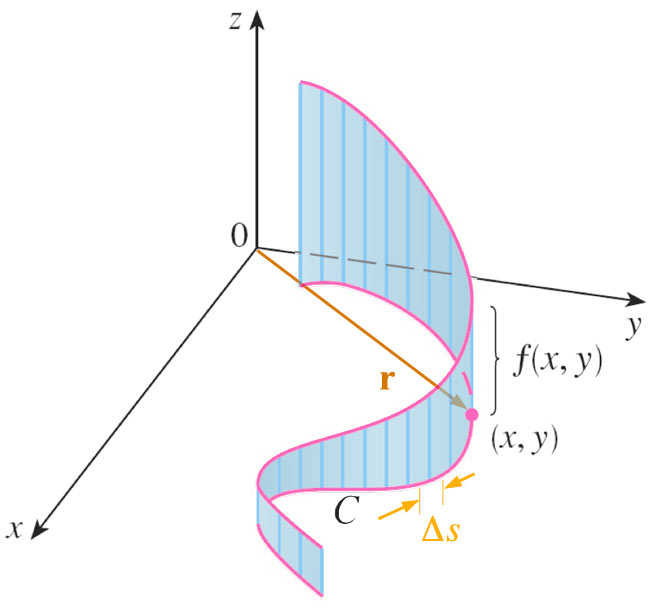
If the curve is chopped up into $n$ arcs...

The line integral of $f$ along $C$ is: $$\int_C f(x,y)\,ds=\lim_{n\to\infty}\sum_{i=1}^n f(x_i^*,y_i^*)\Delta s_i.$$

In section [10.3]--arclength--we found that...

• $\myv r'(t)=\langle x'(t),y'(t) \rangle$ is a vector tangent to the curve.
• [If the parameter $t$ is time, then $\myv r'(t)$ is the velocity vector.]
• The arclength distance traversed when $t$ changes by $\Delta t$ is $$\Delta s\approx |\myv r'|\Delta t=\sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 }\Delta t$$

$$\int_Cf(x,y)\,ds = \int_{t=a}^b f(x(t),y(t)) \sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 } \,dt.$$

Example

$\int \frac yx\,ds$ along the line $x=t^4$, $y=t^3$, $0\leq t \leq 1$.

$$\begineq \int_C \frac yx\,ds &=& \int_{t=0}^1 \frac {y(t)}{x(t)} \sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 } \,dt\\ &=& \int_{t=0}^1 \frac {t^3}{t^4} \sqrt{ \left( 4t^3\right)^2+\left(3t^2\right)^2 } \,dt\\ &=& \int_{t=0}^1 \frac {1}{t} \sqrt{ 16t^6+9t^4 } \,dt\\ &=& \int_{t=0}^1 t \sqrt{ 16t^2+9 } \,dt\\ \endeq $$

Substitution of variables: $u=16t^2+9$, so $du=32t\,dt$:

$$\begineq \int_C \frac yx\,ds &=& \frac{1}{32}\int_{u(0)}^{u(1)} \sqrt{ u } \,du\\ &=& \frac{1}{32}\[ \frac 23 u^{3/2} \]_9^{25} = \frac{1}{16*3}(125-27)=\frac{49}{24} \endeq $$

Example

$$\int_C(x+y^2)ds$$ where $C$ is the line from $(0,0)$ to $(3,0)$.

• Along this line, $y=0$ so $x+y^2\to x$.
• $C$ is along the $x$-axis. Let's use $x$ as our parameter.
• Along the $x$-axis $ds=dx$.

$$\int_C(x+y^2)ds = \int_{x=0}^3x\,dx = \frac 92.$$

Example

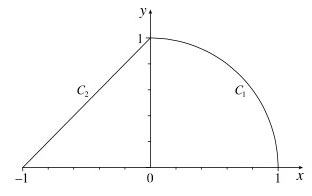$\int (x+y)\,ds=?$

This can be split into two integrals...

Let's do the integral along $C_1$ in polar coordinates, that is our parameter will be $\theta$.

• $x=r\cos\theta;\ \ y=r\sin\theta$. But since $r=1$, we have $x=\cos\theta;\ \ y=\sin\theta$.
• Arclength $$\begineq ds&=&\sqrt{ \left(\frac{\del\, \cos\theta}{\del\theta}\right)^2 + \left(\frac{\del\, \sin\theta}{\del\theta}\right)^2 }\,d\theta \\ &=&\sqrt{ \left(-\sin\theta \right)^2 + \left(\cos\theta\right)^2 }\,d\theta \\ &=&d\theta \endeq $$

Putting these pieces together, $$\int_{C_1} (x+y)\,ds =\int_{\theta=0}^{\pi/2}\left( \cos\theta + \sin\theta \right)\,d\theta=2.$$

Along $C_2$: The equation of the line is $y(x)=x+1$. Let's use $x$ as our parameter... $$ds=\sqrt{ \left(\frac{\del x}{\del x}\right)^2+\left(\frac{\del(x+1)}{\del x}\right)^2 }dx=\sqrt 2\,dx$$

$$\begineq \int_{C_1} (x+y)\,ds &=& \int_0^1 (x+(1+x))\sqrt 2\,dx\\ &=&\sqrt 2 \int_0^1 (1+2x)\,dx=\sqrt 2\[ (x+x^2)\]_0^1=2\sqrt 2. \endeq $$

Line integrals - 3D

$$\begineq \int_Cf(x,y,z)\,ds&=&\int_{t=a}^bf(\myv r(t))\,ds\\ &=&\int_a^bf(x(t),y(t),z(t))\sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 +\left(\frac{\del z}{\del t}\right)^2 }\,dt \endeq $$

Parameterizing a line segment

Many problems will ask you to "integrate along the straight line segment from point $P_1$ to $P_2$".

Here's how we parameterized such a line segment earlier in the course:

• Let $\myv r_1$ be the position vector pointing to $P_1$ and
• $\myv r_2$ be the position vector pointing to $P_2$
• A parametric equation for the directed line segment from $P_1$ to $P_2$ is: $$\myv r(t)=(1-t)\myv r_1+t\myv r_2=\myv r_1+t(\myv r_2-\myv r_1)$$ with $0\leq t \leq 1$.

E.g. the line segment from (1,2,1) to (1,1,3) is: $$\begineq\myv r(t)&=&(1-t)\langle 1,2,1\rangle+t\langle 1,1,3\rangle\\ &=&\langle 1,2,1\rangle +t\langle 1-1,1-2,3-1\rangle\\ &=&\langle 1,2-t,1+2t\rangle=\uv i+(2-t)\uv j+(1+2t)\uv k \endeq $$

To Do

• Scalar line integrals

Image credits

Martin