Vector Line Integrals
...are useful in calculating the work $\approx \sum \myv F_i\cdot \Delta s_i$ when moving in a force field.
Hollywood version of fighting a force field!!!
This is no longer science fiction: We have actually long been such an advanced society that even our young children are able to routinely press forward as they face down invisible force fields!!!
...such as the gravitational force field near Earth's surface
$$\myv F_g(x,y,z)=-mg\uv k.$$
Calculating the work
The work, $\Delta W$, (units of energy) done by a force, $\myv F$ acting on a particle, which moves a distance $\Delta \myv s$: $$\Delta W = \myv F \cdot \Delta \myv s$$In a force field the force acting on a particle, $\myv F=\myv F(x,y,z)$, depends on position.
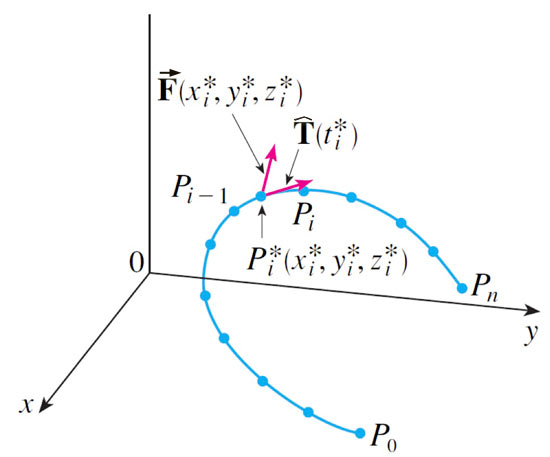A particle moves along the curve $C$ specified by $\myv r(t)$ shown.
The position is given as $P_i=\myv r(t_i)$. In one time-step, it moves a
distance $\Delta \myv s_i=\myv r(t_i)-\myv r(t_{i-1})$.
The work done by the field is $\Delta W_i=\myv F(x_i,y_i,z_i)\cdot\myv \Delta \myv s_i$, so... $$W\approx\sum_{i=1}^n\myv F(x_i^*,y_i^*,z_i^*) \cdot\uv T(x_i^*,y_i^*,z_i^*)\Delta s_i$$ where $\Delta s_i$ is the distance moved in interval $i$, and $\uv T$ is the unit tanget vector.
In the limit $n\to\infty$ the sum becomes an integral, the line integral of $\myv F$ along $C$: $$W=\int_C\myv F\cdot\uv T\,ds=\int_C \myv F\cdot d\myv r = \int_{t=a}^b\myv F(t)\cdot \myv r'(t)\,dt.$$
Sign convention for work
We tend to think about the energy (=work) needed from the point of view of a child / a car / the starship Enterprise as it fights against a force field. This is just (-1) $\times$ the work that the force field does on the child / car / Enterprise.
So, to avoid having to carry a negative sign around through all these calculations, we'll take the point of view of the "Klingons" who have to pay the energy bill when their force field pushes against the starship Enterprise.
A man dressed as a Klingon carrying a negative sign around. Maybe he's mixed up about his point of view on work?
$$dW = \myv F \cdot d\myv s=\myv F\cdot\myv r'(t)\,dt
=|\myv F| \,|\myv r'(t)| \cos \theta \,dt.$$
Positive, zero, negative dot products
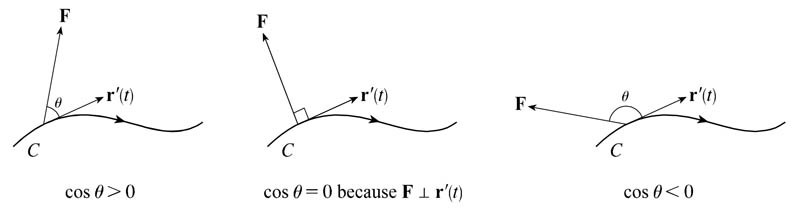
Positive, negative, or zero?
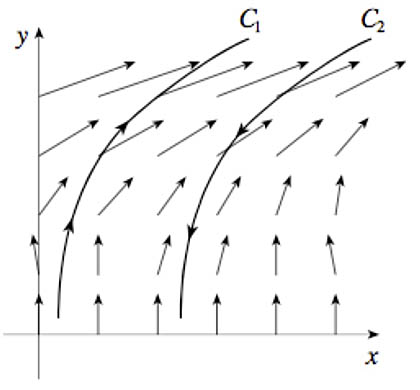$\int_{C_1}\myv F\cdot d\myv r\ \ $?
$\int_{C_2}\myv F\cdot d\myv r\ \ $?
To do
- Visualizing Vector Line Integrals
Example
Find the work done by the vector force field $$\myv F = (y-x^2)\uv i + (z-y^2)\uv j +(x-z^2)\uv k$$
...over the oriented curve
$\myv r(t)=t\uv i +t^2\uv j+t^3\uv k$
from $(0,0,0)$ to $(1,1,1)$.
$$W=\int_{t=0}^1\myv F(t)\cdot \myv r'(t)\,dt.$$
Computing example
Find the work done by the vector force field $$\myv F = x\uv i +z \uv j + y\uv k=P\uv i + Q\uv j+R\uv k$$
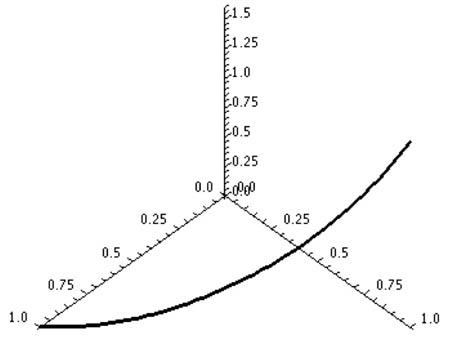...over the oriented curve
$\myv r(t)=\cos t \uv i +\sin t \uv j +t\uv k$
for $0\leq t \leq \frac\pi 2$.
$$W=\int_{t=0}^0\myv F(t)\cdot \myv r'(t)\,dt.$$
Line integral in differential form
In the limit $n\to\infty$ the sum becomes an integral, the line integral of $\myv F$ along $C$: $$W=\int_C\myv F\cdot\uv T\,ds=\int_C \myv F\cdot d\myv r = \int_{t=a}^b\myv F(t)\cdot \myv r'(t)\,dt.$$
A vector field can always be expressed abstractly in terms of its $x$, $y$, and $z$ components: $$\myv F(x,y,z)=P(x,y,z)\uv i +Q(x,y,z)\uv j +R(x,y,z)\uv k.$$ [$P$, $Q$, $R$ is a way of avoiding the double meaning of $F_x$, $F_y$, $F_z$...]
We've been solving these line integrals, by parameterizing the curve, and using the last expression:
$$\int_{t=a}^b\myv F(t)\cdot \myv r'(t)\,dt.$$
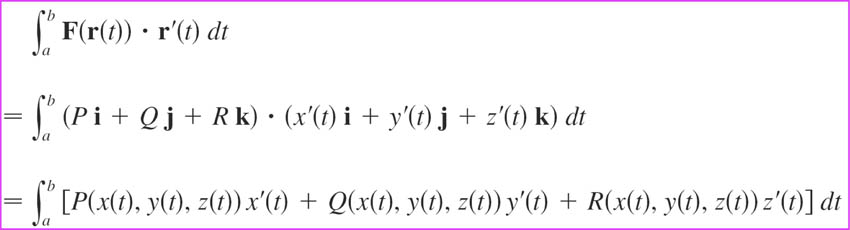
But the next-to-last expression $$\int_C \myv F\cdot d\myv r,$$ can also be used to calculate line integrals.
The vector differential $d\myv r$ means: $$d\myv r\equiv dx\,\uv i +dy\,\uv j+dz\,\uv k.$$
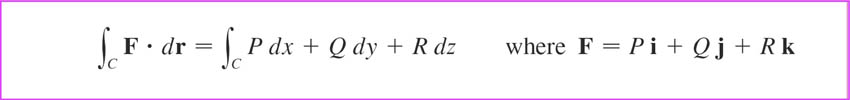
Clearer(?) to write this as: $$\int_C\myv F\cdot d\myv r=\int_c P\,dx +\int_c Q\,dy +\int_c R\,dz.$$
Example
$$\myv F(x,y)=x\uv i+x^2\uv j.$$ where $P(x,y)=x$ and $Q(x,y)=x^2$.
Three paths from $(-1,0)$ to $(0,1)$.
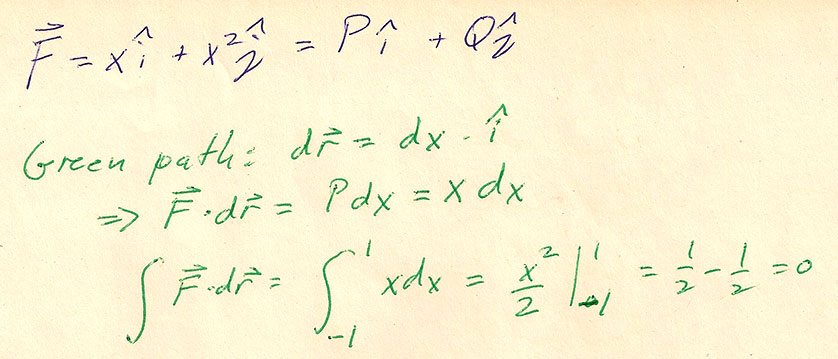
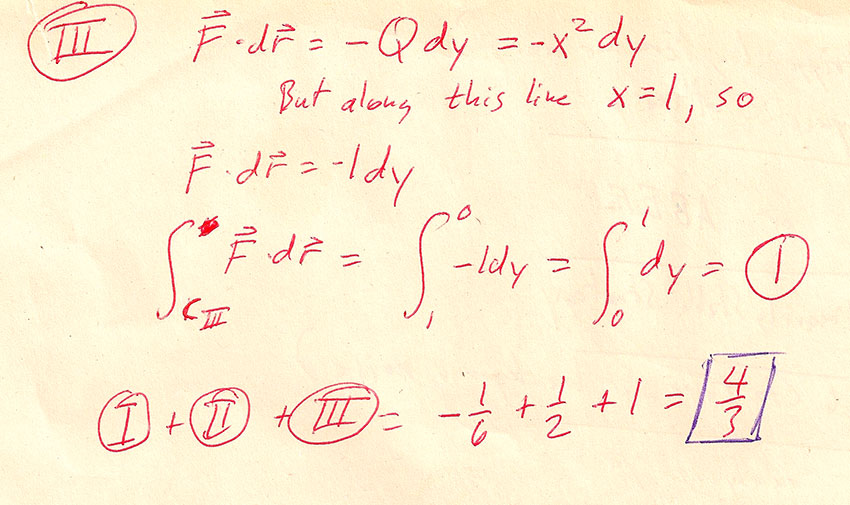
To Do
- Compute the line integral of $\myv F=x^2\uv i+y^4\uv j+z^6\uv k = P\uv i+ Q\uv j +R\uv k$ over the path $\myv r_1: x=t^3, y=t, z=t^2, 0 \leq t \leq 1$.
- Compute the line integral of the same vector field $F$, but this time over the path $\myv r_2 : x=y=z=t, 0\leq 0 \leq 1$.