The Divergence Theorem


Io passing in front of Jupiter, NASA - Cassini mission.

Gravitational force on a mass $m$ at $\myv r$ due to mass $M$ at the origin: $$\myv F_g=-G\frac{mM}{r^2}\uv r$$ Electrical force on a charge $q$ at $\myv r$ due to a charge $Q$ at the origin: $$\myv F_e=q\myv E(\myv r)=-k\frac{qQ}{r^2}\uv r$$ These are both derivable from a potential function, $f$ that looks like: $$f(\myv r)=C\frac 1r,$$ where $\myv F(\myv r)=-\myv \grad f(\myv r)$. It turns out that

Hideki Yukawa generalized this potential to encompass nuclear forces as well, which pretty much have no effect beyond a range of order $10^{-15}$m $$f(\myv r)=C\frac{e^{-r/r_0}}{r}$$ where $r_0$ is the "range" of the force and $r_0\propto 1/m_b$. Each field has a boson which is the particle that "mediates" the field.

  • For electromagnetism, the particle is the photon, which is massless.
  • For the gravitational field, the particle would be the graviton....
  • For nuclear forces, Yukawa was proposing massive mesons.

It turns out that if you know the electric field, $\myv E$, you can find the charge density from: $$\myv \grad\cdot\myv E=\rho(\myv r)/\epsilon_0.$$.

Green's Theorem: flux integral

Recapping Green's Theorem in terms of the normal component of a vector field $F$ in the $xy$ plane:

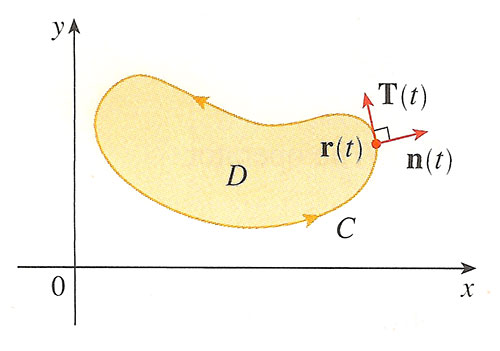
We found that

$$\oint_C \myv F\cdot \uv n\,ds = \iint_D \myv \grad \cdot \myv F \,dA. $$

  • The l.h.s. is the flux of $\myv F$ through the boundary
  • $\myv \grad\cdot \myv F \equiv \left( \frac{\del P}{\del x}+\frac{\del Q}{\del y} \right)$ is the divergence of the vector function, $\myv F(x,y)$ in 2 dimensions.

The Divergence Theorem

...is a generalization of that 2-d result to 3 dimensions:


Or,

$$\oiint_S\myv F\cdot d\myv S=\iiint_E \myv \grad \cdot \myv F\,dV $$

  • The ∯ symbol means a surface integral over a closed surface.
  • $d\myv S=\uv n\,dS$ is a vector differential which is everywhere normal to the surface.
  • The divergence at a point is something like the local 'flux density'.

Paraphrase: The volume integral of the flux density over a solid region is equal to the total flux through the surface bounding that region.

Example

Calculate the total flux, $\oiint_S \myv F\cdot \uv n \,dS$ through *all* the surfaces enclosing the volume bounded by the triangle (which intersects each axis 9 units from the origin), and the planes $x=0$, $y=0$, $z=0$, where the vector field is: $$\myv F(x,y,z)=(x+y^2)\uv i+(y+z^2)\uv j+(z+x^2)\uv k=P\uv i+Q\uv j+R\uv k.$$

There are 4 surfaces.

Let's start with the toughest looking, triangular face. We'd like calculate the flux through the surface

$\iint_S \myv F\cdot \uv n \,dS$

where $S$ is the surface with vertices $(9,0,0)$, $(0,9,0)$, $(0,0,9)$,

I'll use this form of the surface integral: $$\iint_S f(x,y,z)\,dS= \iint_D f(x,y,g(x,y))\sqrt{1 + \left(\frac{\del g}{\del x}\right)^2 +\left(\frac{\del g}{\del y}\right)^2 }\,dx\,dy.$$

The equation of the plane containing the triangle is.. $$x+y+z=9 \Rightarrow z=g(x,y)=9-x-y$$

  • $g_x=g_y=-1$ so the square root factor is $\sqrt{3}$
  • the limits of integration are $$\iint_D=\int_{x=0}^9\int_{y=0}^{9-x}$$

The function $f(x,y,z)=f(x,y,g(x,y))$ in the integral is $\myv F\cdot\uv n$.

  • The unit normal vector to the plane is $\uv n=\frac{1}{\sqrt 3}\langle 1,1,1\rangle$,
  • so $$\myv F\cdot \uv n = \frac{1}{\sqrt 3} \left(x+y^2+y+z^2+z+x^2\right)$$
  • substituting in $z=9-x-y$ on the triangular surface, Mathematica expands this to... $$\myv F\cdot\uv n = \frac{1}{\sqrt 3}(90 - 18 x + 2 x^2 - 18 y + 2 x y + 2 y^2)$$

Putting this all together... $$\begineq \iint_D\myv F\cdot \uv n dS &=& \frac{1}{\sqrt 3}\int_{x=0}^9\int_{y=0}^{9-x}(90 - 18 x + 2 x^2 - 18 y + 2 x y + 2 y^2)\,dy\,dx\\ &=&\frac{8019}{4\sqrt 3}\endeq$$ $$

Oh no, I've still got 3 more surfaces to integrate over!!

Example, v 2.0

Calculate the total flux, $\oiint_S \myv F\cdot \uv n \,dS$ through *all* the surfaces enclosing the volume bounded by the triangle (which intersects each axis 9 units from the origin), and the planes $x=0$, $y=0$, $z=0$, where the vector field is: $$\myv F(x,y,z)=(x+y^2)\uv i+(y+z^2)\uv j+(z+x^2)\uv k=P\uv i+Q\uv j+R\uv k.$$

Using the divergence theorem, we could write the desired integral as... $$\oiint_S \myv F \cdot \uv n\, dS = \iiint_E \myv \grad \cdot \myv F \,dV.$$

The divergence is $$\myv \grad \cdot \myv F =\frac{\del P}{\del x}+\frac{\del Q}{\del y} +\frac{\del R}{\del z}= 1+1+1=3.$$

So, $$\iiint_E \myv \grad \cdot \myv F\, dV=3\iiint_E\,dV=3*(9*9/2)(9)/3=729/2.$$

Check the divergence theorem for our function and box of 13.4.