Comparing Heat pumps

  • What's the best an ideal heat pump could do?
  • Taking the local weather into account...What do SEER and HSPF mean?
  • Actual performance of heat pumps...

Evaluating heat pumps

A heat pump can be used to heat your house. Either instead of a furnace (mild climate) or in addition to a furnace (N. IN).They move thermal energy...

  • from a "low temperature" place, either outside air ("air source" heat pump) or water below ground ("ground source" heat pump),
  • to a "high temperature" place: inside of your house.

In the summer, you reverse the pumping of heat.. the cold temperature place is inside, and you pump heat to the outside (warmer). This is called "air conditioning"!

A gas furnace converts the chemical energy of the fuel to heat, and cannot have an efficiency more than 1.

A heat pump can theoretically transfer *more* heat energy than the electrical energy used to move the heat. But how much?

Heat pumps can be compared based on their "Coefficient of Performance", COP, which is a unitless ratio of heat delivered to the hot place / energy needed to get it there. $$c_\text{hp}=\frac{\text{Heat (energy) delivered}} {\text{Energy to *move* the heat}}.$$ In a course or unit on Thermodynamics, we would demonstrate that for an ideal ("Carnot") heat engine, the maximum coefficient of performance is a simple function of the absolute (degrees Kelvin above absolute zero) temperatures: $$c_\text{hp}=\frac{T_2}{T_2-T_1}.$$ where,

  • $T_1$ is the temperature of the colder "reservoir" from which we're pulling heat and
  • $T_2$, the target temperature inside the house that you're heating:
Calculate $c_\text{hp}$ for $T_2=68$ F and
  • $T_1 = 35$ F, the average temperature of air on a mild winter day with a low of freezing and a high of 42 F).
  • $T_1 = 25$ F, the average temperature of air on a fairly cold winter's day in Goshen.
  • $T_1 = 54$ F, the average temperature of groundwater 2 m down in Goshen throughout the winter.

Here are your calculations for $c_{hp}$ for these three different temperature combinations:

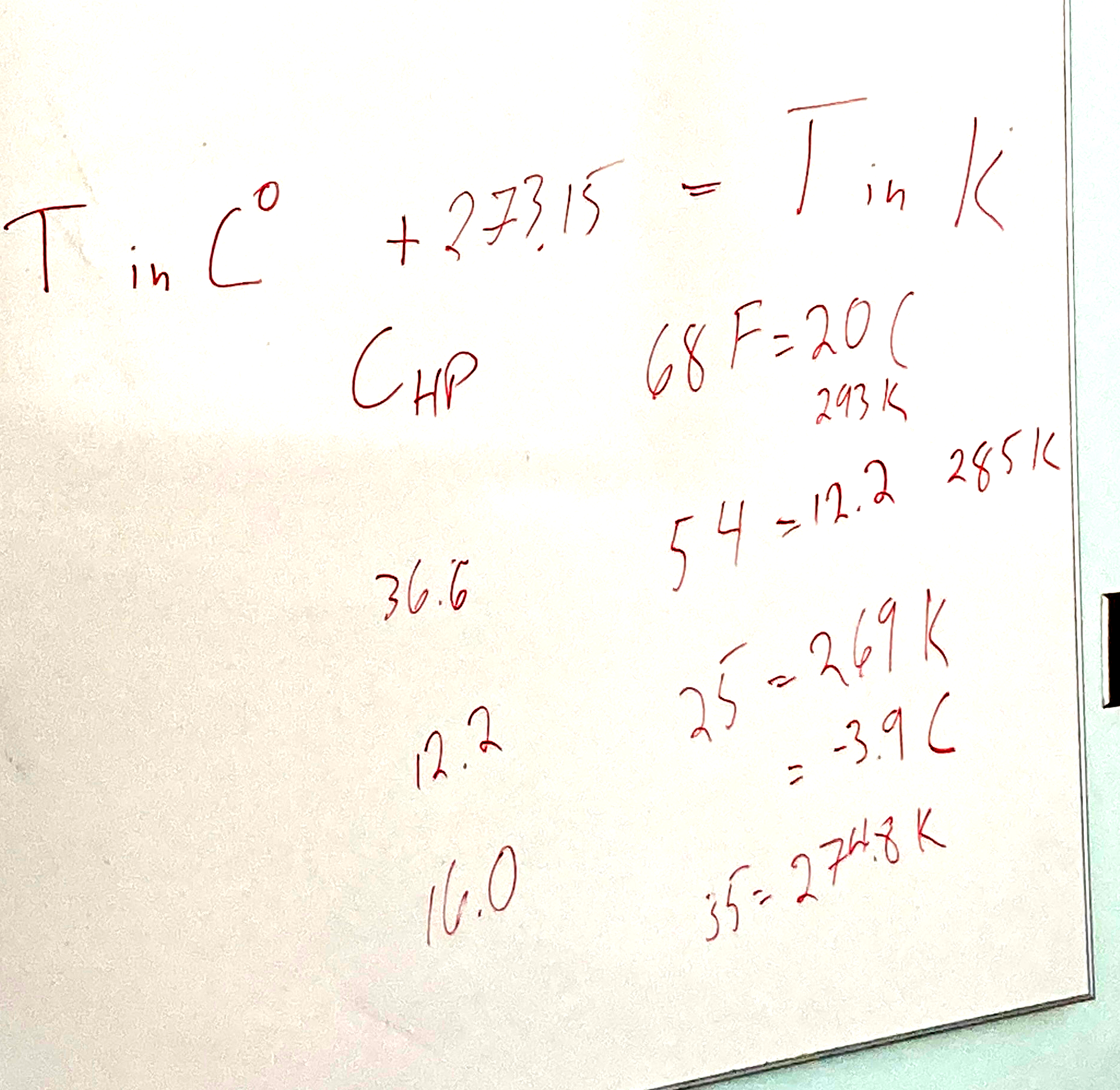
The meaning of the last row: An ideal heatpump would be able to move 16 Joules of heat for every 1 Joule of electricity when pulling heat out of a reservoir at 35 F and transferring that heat into a house at 68 F.

The heat pump is 16 $\times$ better than just running the electricity through a resistor inside the house ("resistive heating") and converting the electrical energy directly into heat energy.

But unfortunately, heat pumps (and air conditioners) use a different ratio whic is *not* unitless. One is HSPF and one is SEER. In groups:

  1. Each group will pick one manufacturer out of American Standard / Bryant / Carrier / Lennox / Rheem / Trane. Find the HSPF and SEER values for a top-of-the-line model of air-source heat pump. Get a cost too, if they list one.
  2. Find the HSPF and SEER values for their entry-level model. Get a cost too, if they list one.
  3. Find the units of HSPF and SEER, and their meaning. One is used for heating, one is used for cooling. Which is which?

    Both have units of "Heat delivered to hot reservoir (BTU)"/"Electric energy used (Watt$\cdot$hours)".

  4. Figure out how to convert those units to the unitless COP ratio. Re-state your values in terms of COP.

    HSPF (and SEER) both have units of BTUs per Watt$\cdot$hour. Both BTUs (British Thermal Units) and Wh are units of energy, but they are different units of energy. $c_{hp}$ is a unitless ratio of heat energy delivered divided by electricity consumed.

    Since there are 3.41 BTU / Wh, $$c_{hp}=\text{HSPF:}\frac{\text{BTU}}{\text{Wh}}*\frac{1\text{ Wh}}{3.41\text{ BTU}}$$

Here are the results of your internet searches for HSPF (heating seasonal performance factor) and SEER ("seasonal energy efficiency rating"... refers to air conditioning performance).

The numbers in black are the manufacturer's HSPF and SEER ratings in BTU/Whr.
The numbers in blue are the unitless $c_{hp}$ and $c_\text{refrigeration}$ ratios.

Taking into account the weather

HSPF is supposed to be heating performance averaged over some statistically average heating season for the USA. (And SEER is cooling performance over a cooling season.) But of course, we'd like to know the performance for our particular climate!

According to this paper, from researchers at FSEC and UC-Berkeley we're roughly ARI climate zone IV [A(H)RI: Air conditioning, Heating, and Refrigeration Institute - HVAC industry trade group]

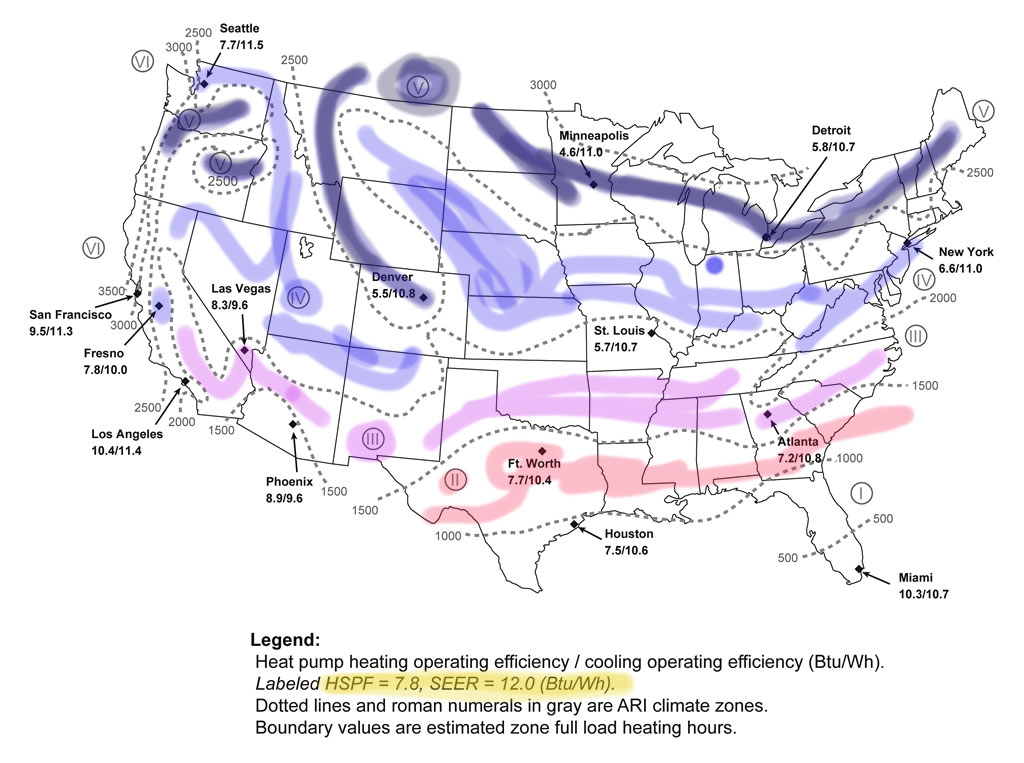
To interpret this map: A heat pump with an HSPF of 7.8 and a SEER of 12.0 actually performs with an HSPF/SEER values of 6.6 and 11.0 in New York city's average climate.

That same heat pump in Miami would have HSPF/SEER values of 10.3/10.7 in Miami.

These HSPFs are for air source heat pumps! Ground source heat pumps will do better because they are operating (in Goshen) with an outside reservoir of about 54 F year-round!