Cross product [9.4]

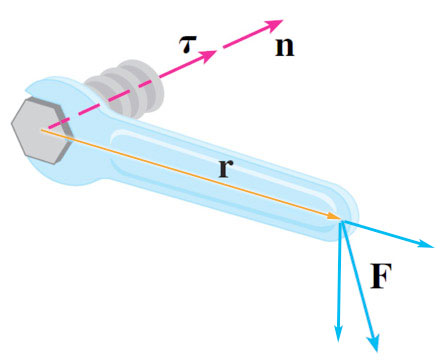
Torque
With the dot product, we considered the best angle of a force relative to direction of motion when pushing a cart.
Now we'd like to tighten a bolt with a wrench and again we'll pay particular attention to an angle...
There are several factors:
- The force, $F$, exerted on the wrench,
- the distance, $r$, from the bolt, along the handle to the point where the force is applied matters.
- Angle: The orientation of the force with respect to the wrench handle:
- Pushing the handle directly towards or away from the bolt has no effect.
- Pulling at right angles to the handle seems to be most effective.
- At intermediate angles there is some effect but less than at right angles.
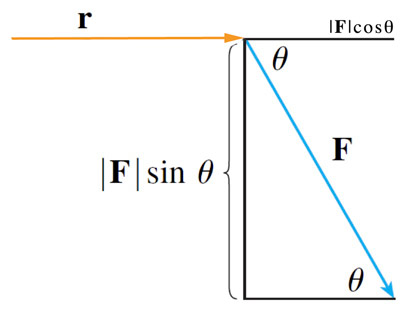 Which component of the force--parallel or perpendicular to $\myv r$--is more effective at tightening bolts?
Which component of the force--parallel or perpendicular to $\myv r$--is more effective at tightening bolts?
It seems like this combination of factors is related to the "effectiveness of turning bolts": $$|\myv r||\myv F|\sin \theta\equiv \tau$$ $\tau$ is called the 'torque'. In the diagram above $\tau$ is the magnitude of a vector which is perpendicular to $\myv r$ and $\myv F$.
Meaning of the direction of $\myv \tau$? $\myv \tau$ is parallel to the axis of the bolt. $\myv \tau$ points in the direction that a standard, right-hand threaded bolt would advance when turned clockwise ($\equiv$ "righty tighty"!).
We conclude that $$\tau = rF\sin\theta \nonumber$$ to motivate the...
Definition of the cross product
If $\myv a$ and $\myv b$ are non-zero 3-d vectors, then the cross product $\myv a \times \myv b$ is: $$\myv a \times \myv b \equiv |\myv a| |\myv b| \sin \theta\, \uv n,$$
- $\theta$ is the smaller angle between $\myv a$ and $\myv b$ ($0\leq\theta\leq \pi$)
- $\uv n$ is a unit vector
- perpendicular to $\myv a$ and $\myv b$
- according to the right-hand rule: Curl r.h. fingers from $\myv a$ towards $\myv b$ and your thumb points in the same direction as $\uv n$.
Geometry
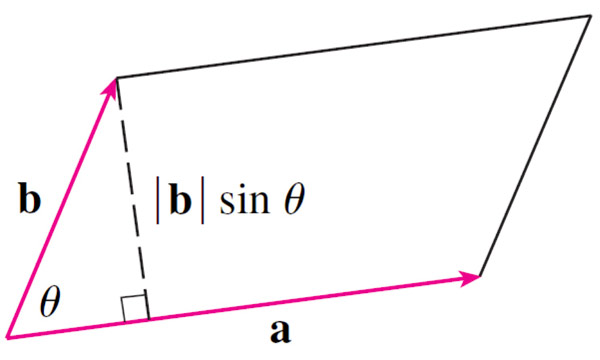
The magnitude of the cross product, $|\myv a \times \myv b|=ab\sin\theta$, is the same as the area of the parallelogram determined by $\myv a$ and $\myv b$.
See www.geogebra.org/m/hjgxmz5a
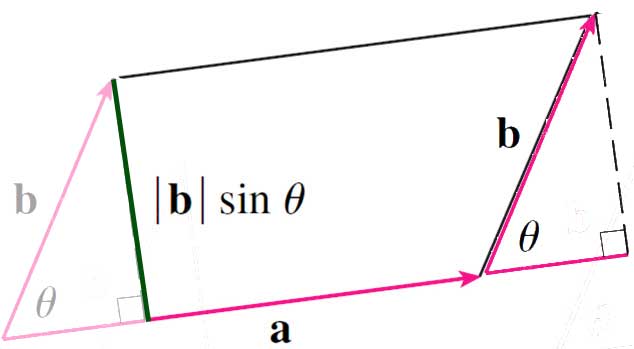
Do Schlicker problem 5. Some guidance: We just looked at how to find the area of a parallelogram. Sketch generically two vectors $\myv a$ and $\myv b$ with their tails touching. What is the relationship of the area of the parallelogram defined by $\myv a$ and $\myv b$ and the area of the triangle with sides $\myv a$, $\myv b$, and as the third side, a line segment from the tip of $\myv a$ to the tip of $\myv b$?
Cross product: order matters!
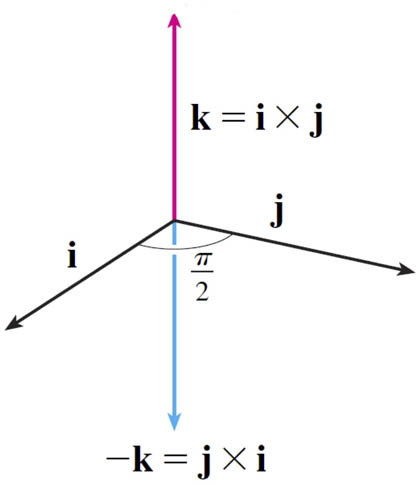 With the right-hand rule, the order of the vectors in the cross product matters.
With the right-hand rule, the order of the vectors in the cross product matters.
Properties

The last two relations give us a way of computing the cross product from its components...
Computing the cross product
Grinding out the cross product from its components...
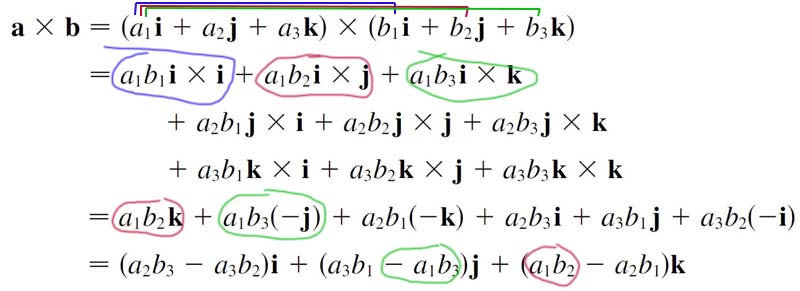
It's not at all obvious that this is the same as $ab\sin\theta\,\uv n$. But Schlicker demonstrates "through some significant algebra" that the magnitudes of our two expressions are the same.
Cross product: Remembering with the determinant
I remember how to compute the cross product by using the determinant of this 3$\times$3 matrix: $$\myv a \times \myv b = \text{det}\left| \begin{array}{ccc} \uv i & \uv j & \uv k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|.$$
To compute the determinant,
add the red products,
and subtract
the blue products
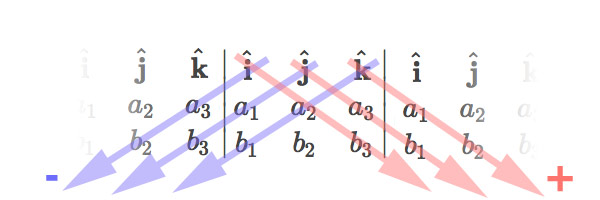
$$\myv a \times \myv b=(a_2b_3-a_3b_2)\uv i + (a_3b_1-a_1b_3)\uv j+(a_1b_2-a_2b_1)\uv k.\nonumber$$
For example: $\myv a=\langle 1,-2,-4 \rangle$ and $\myv b=\langle 2,4,8\rangle$ $$\begineq \myv a \times \myv b &= \det\left| \begin{array}{ccc} \uv i&\uv j&\uv k \\ 1 & -2 & -4 \\ 2 & 4 & 8 \end{array} \right|\\ &= (-2*8 -(-4*4))\uv i+ (-4*2-(1*8))\uv j+ (1*4-(-2*2))\uv k\\ &= -16\uv j +8\uv k=\langle 0, -16,8\rangle.\nonumber \endeq $$
Do AC problem 5 once more! But this time use the algebraic way of evaluating the cross product and check that you get the same answer.
Triple products
There are many ways to form triple products. Of these, which are vector or scalar quantities or neither?
- $\myv a \cdot (\myv b \cdot \myv c)$
- $\myv a \cdot (\myv b \times \myv c)$
- $\myv a \times (\myv b \cdot \myv c)$
- $\myv a \times (\myv b \times \myv c)$
Scalar triple product
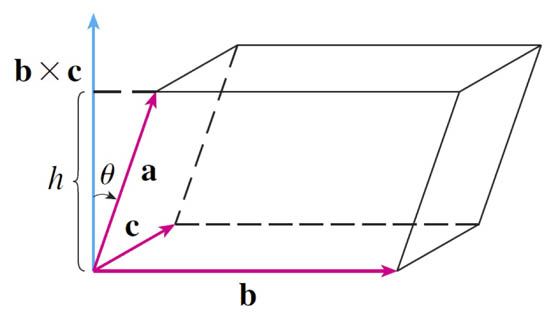
The volume of the parallelipipid determined by $\myv a$, $\myv b$, and $\myv c$ is: $$V= h B$$ Where $B$ is the area of the base (defined by $\myv b$ and $\myv c$) and $h$ is the height of the parallelipid above its base. [Are extremes plausible...?] Now...
- height is $h=|\myv a| \cos\theta$ where $\theta$ is the angle to the vector direction which is perpendicular to the base.
- area of the base is $B=|\myv b \times \myv c|$.
...and $\myv b \times \myv c$ is a vector perpendicular to the base, as shown, with the magnitude of $B$.
So, the volume can be written as $$V=|\myv a|\cos\theta |\myv b \times \myv c| = \myv a \cdot (\myv b \times \myv c).$$
[Without proof] This may also be calculated from: $$\myv a \cdot (\myv b \times \myv c) = \text{det}\left| \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right|$$
Vector triple product
$$\myv a \times (\myv b \times \myv c) =(\myv a \cdot \myv c)\myv b -(\myv a \cdot \myv b)\myv c.$$
Perpendicular to $\myv a$
Consider the set of all vectors $\myv b$ and $\myv c$ such that $\myv b \times \myv c = k \myv a$. (a scalar multiple of $\myv a$). What geometrical entity do these vectors form?
To do
- Messing around with the cross product.