Polar integrals [11.5]

Kakslauttanen Igloo Village, Finland
Area in Cartesian coordinates
In Cartesian coordinates...

Consider...
- the path traced out by increasing the $x$ coordinate of a position vector by an amount $\Delta x$.
- the path traced out by increasing the $y$ coordinate of a position vector by an amount $\Delta y$.
These two paths define a parallelogram with an area $\Delta A = \Delta x\,\Delta y$
One thing you may take for granted...
- No matter where we we are in the $xy$ plane, $\Delta A =\Delta x\,\Delta y$
As the changes get small--$\Delta x\to dx$ and $\Delta y\to dy$--the differential of area is $$dx\,dy = dA.$$
Area in Polar coordinates
We reviewed polar coordinates (briefly). We can readily see that: $$\Delta \theta\, \Delta r \neq dA,$$ since the units don't work out: $\Delta r$ is a length (for example, in cm); But $\Delta \theta$ has units of radians.
Considering changes in polar coordinates in more detail...

- Increasing the coordinate $r$ by an amount $\Delta r$ traces out a path of length $\Delta r$.
- But increasing the coordinate $\theta$ by an amount $\Delta \theta$ causes the position vector to trace out a path of length $r\Delta \theta$, which depends on the distance $r$ from the origin.
The area of the shaded region is a bit odd-shaped. But as changes in the coordinates get very small--that is $\Delta \theta \to d\theta$ and $\Delta r\to dr$--the area becomes more nearly rectangular (see this desmos diagram), with sides of length $r\,d\theta$ and $dr$, so...
Differential of area in polar coordinates: $$dA=(r\,d\theta)\,dr=r\,dr\,d\theta.$$
Area of a circle
Wouldn't it be nice? ...if we could find areas in polar coordinates using an iterated double integral together with our recently derived $dA$?
Let's try to find the area of a circle of radius $R$ (you know the answer) like this: $$\begineq A &=\iint_A\,dA\endeq$$
We'd have to define the limits on the integrals in polar coordinates.
Think of a position vector in polar coordinates, $\myv r=\myc{ r,\theta}$. What are all the possible values of $r$ and $\theta$ for points inside a circle of radius $R$? This leads to the following limits...
$$\begineq \iint_A\,dA&=\int_{\theta=0}^{2\pi}\int_{r=0}^R r\,dr\,d\theta \\
&=\int_{\theta=0}^{2\pi}\left( \left. \frac{r^2}{2} \right|_0^R\right)\,d\theta\\
&=\frac{R^2}{2}\int_{\theta=0}^{2\pi}d\theta=\frac{R^2}{2}2\pi = \pi R^2.
\endeq
$$
Double polar integrals.
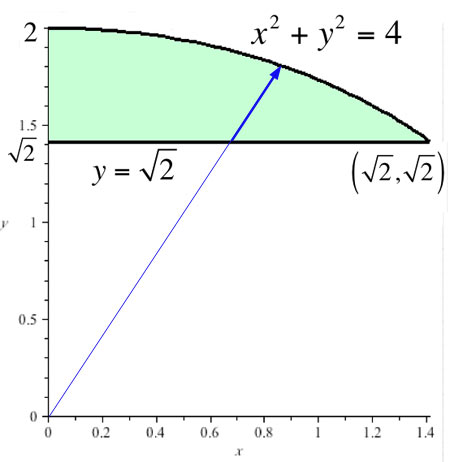
$A=\iint_A f(r,\theta)\,dA=?$
Double polar integrals..
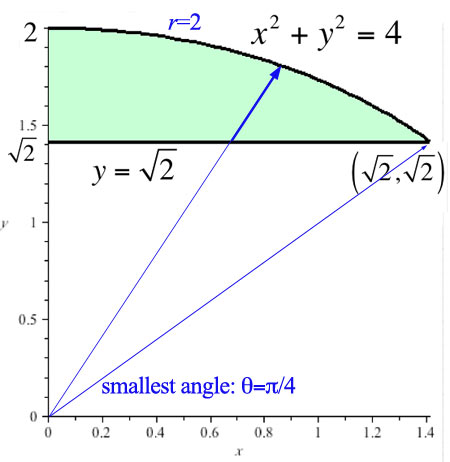
$A=\iint_A f(r,\theta)\,dA=?$
The line $\sqrt 2=y=r\sin\theta$ becomes
$r(\theta)=\frac{\sqrt 2}{\sin\theta}=\sqrt 2 \csc\theta$.
The double integral becomes: $$A=\int_{\theta=\pi/4}^{\pi/2} \int_{r=\sqrt 2\csc\theta}^2 f(r,\theta)\,r\,dr\,d\theta.$$
Converting...
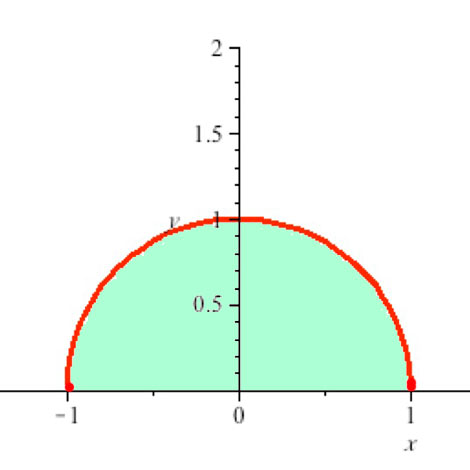
Converting a double-integral in Cartesian coordinates to polar coordinates:
$\iint_A e^{x^2+y^2}dA=\int_{x=-1}^1\int_{y=0}^{\sqrt{1-x^2}}e^{x^2+y^2}dy\,dx=...$
- $r$ runs from 0 to 1.
- $\theta$ runs from 0 to $\pi$.
- ah, $x^2+y^2=r^2$
- $dx\,dy=dA=r\,dr\,d\theta$
$$\begineq\iint_Ae^{r^2}dA &=\int_{\theta=0}^{\pi}\int_{r=0}^1e^{r^2}r\,dr\,d\theta\\ &=\int_{\theta=0}^{\pi}\left(\left.\frac{e^{r^2}}{2}\right|_{r=0}^1\right)\,d\theta\\ &= \left(\frac{e-1}{2}\right)\int_{\theta=0}^{\pi}\,d\theta = (e-1)\frac\pi 2 \approx 2.70 \endeq $$
ToDo
11.5 Polar - Double integrals in polar coordinates