[06.3] - Think before you integrate

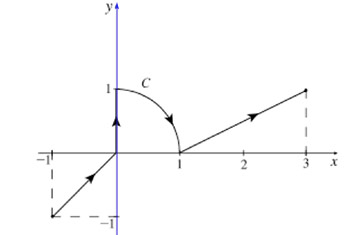
1. Compute $\int_C (ye^{xy}\uv i + xe^{xy}\uv j)\cdot d\myv r$ for the curve $C$ shown below.
   
   

   show / hide solution

   A potential function such that $\myv \grad f=ye^{xy}\uv i + xe^{xy}\uv j)$ is $f(x,y)=e^{xy}$. Therefore, the integral is: $$\int_{\myv r_i}^{\myv r_f} \myv\grad f\cdot d\myv r =f(\myv r_f)-f(\myv r_i),$$ where the curve runs from $\myv r_i=\langle -1,-1\rangle$ to $\myv r_f=\langle 3,1\rangle$. So the answer is $e^{3*1}-e^{-1*-1}$$=e^3-e^1$

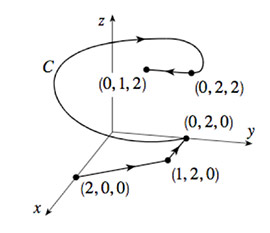
2. Compute $\int_C (yz^2\uv i + xz^2\uv j+2xyz\uv k)\cdot d\myv r$ for the curve $C$ shown below.
   
   

   show / hide solution

   A potential function that gives this vector field is $f(x,y,z)=xyz^2$. So the integral is $f(\myv r_f)-f(\myv r_i)=f(0,1,2)-f(2,0,0)=(0*1*2^2)-(2*0*0)$$=0$.

3. Let $\myv F(x,y)=(2x+y)\cos(x^2+xy)\uv i+\left(x\cos(x^2+xy)+1\right)\uv j$.
   1. Show that $\myv F$ is a conservative vector field.

      show / hide solution

      $$\begineq \frac{\del P}{\del y}&=\frac{\del }{\del y}(2x+y)\cos(x^2+xy)\\ &=1*\cos(x^2+xy) +(2x+y)\sin(x^2+xy)*x\\ \endeq$$ $$\begineq \frac{\del Q}{\del x}&=\frac{\del }{\del x}(x\cos(x^2+xy)+1)\\ &=\cos(x^2+xy) +x\sin(x^2+xy)*(2x+y) \endeq$$ Since these are equal, $\myv F$ is a conservative vector field.

   2. Let $C$ be the curve parameterized by $\myv r(t)=\sin t\uv i+(1-\cos t)\uv j$ with $0\leq t\leq \pi$.
      Find $\int_C \myv F \cdot d\myv r$.

      show / hide solution

      $\myv r_i=\myv r(0)=\sin(0)\uv i +(1-\cos(0))\uv j=(0,0)$, and $\myv r_f=\myv r(\pi)=\sin(\pi)\uv i +(1-\cos(\pi))\uv j=(0,2)$.
      
      A potential function is $f(x,y)=\sin(x^2-2y)$.
      So the integral is $f(0,2)-f(0,0)=-\sin(0^2-4)-(-\sin(0^2-2*0))=-\sin(-4)$
      = -0.757.