[9.3] - Projections & dot product

Read section 9.3 in the textbook and answer these questions.

1. For the two vectors shown, draw the vector projection of $\myv b$ onto $\myv a$.
   
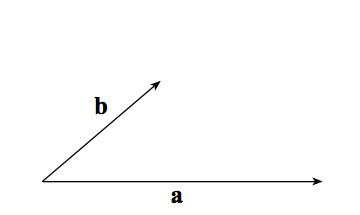
2. For the same two vectors, draw the vector projection of $\myv a$ onto $\myv b$.
   
3. What is the angle between the vectors $\langle 1,0,-1\rangle$ and $\langle 1,1,0\rangle$?

   $$\theta = \arccos(\myv a\cdot\myv b/(ab))=\arccos\left(\frac 1{\sqrt 2*\sqrt 2}\right)=\pi/3= 60{}^o$$

   
   
   
   
4. Suppose that $\myv a \neq 0$ and $\myv a \cdot \myv b=\myv a \cdot \myv c$. This means that $\myv b$ and $\myv c$ have the same projection onto $\myv a$. Does this automatically mean that $\myv b = \myv c$?
   
   Consider $\myv a=\langle 1,2 \rangle$ and $\myv b=\langle 2,1 \rangle$. Show that the answer to the question above is "no", by finding a vector $\myv c$ which is not equal to $\myv b$, but never the less satisfies $\myv a \cdot \myv b=\myv a \cdot \myv c$.