9.3 - The regular Hexagon
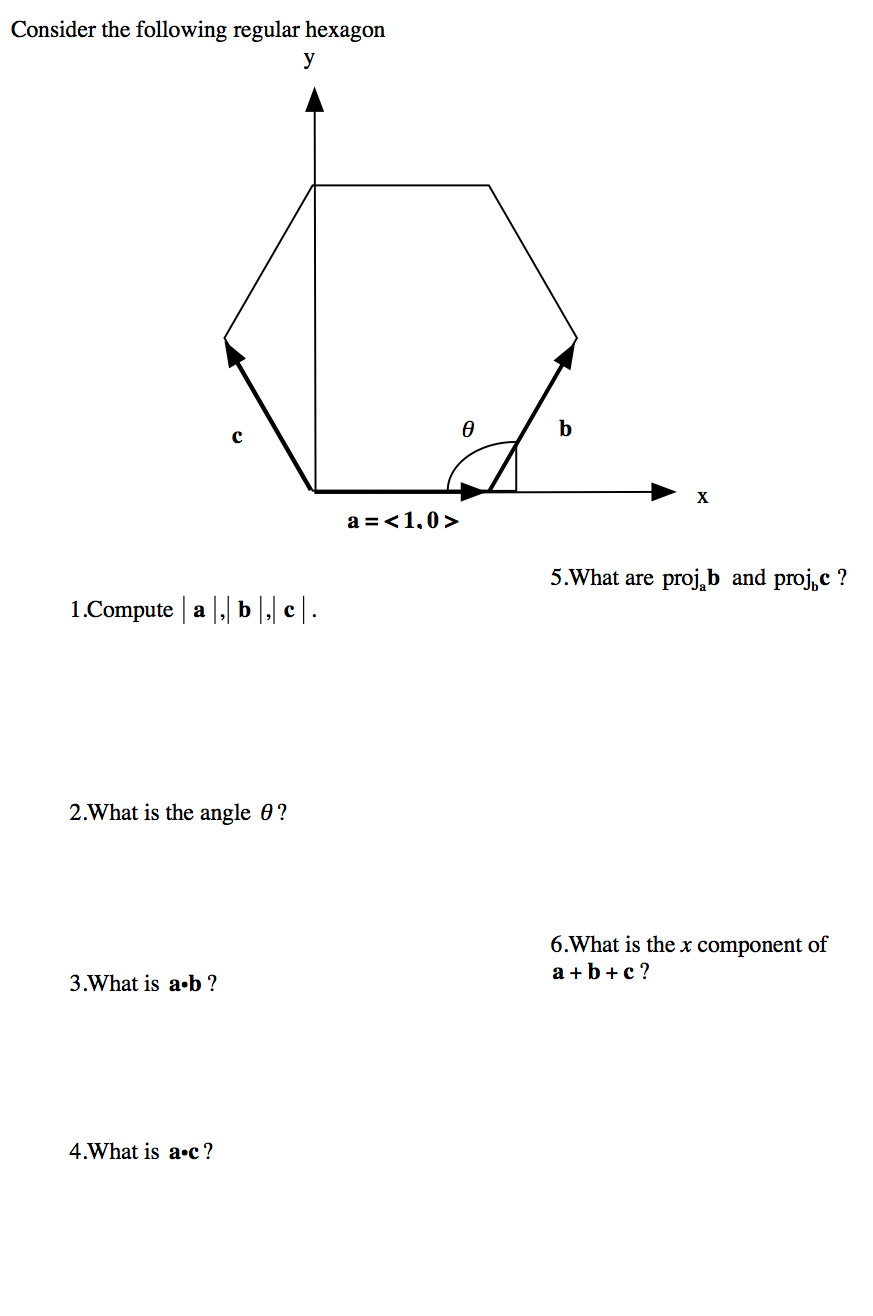
Hints...
- In #3 think carefully about the positions of the vectors and the way the angle between two vectors is defined in the dot product.
- In #6, try sketching the sum visually by drawing the vectors head to tail...
Answers:
- $|\myv a| = \sqrt{1^2+0}=1$. And since all the sides of the regular hexagon are the same length,$|\myv a|=|\myv b|=|\myv c|=1$.
- The angle is 120${}^o$ or $\pi/3$ radians
- If we put $\myv a $ and $\myv b$ tail-to-tail, the angle between them is $60^o$, so $\myv a\cdot\myv b=ab\cos 60^0=1*1*\frac 12 =$ $\frac 12$.
- The angle between $\myv a$ and $\myv c$ is 120${}^o$, and the cosine of that angle is -1/2. So, the dot product is $-\frac 12$.
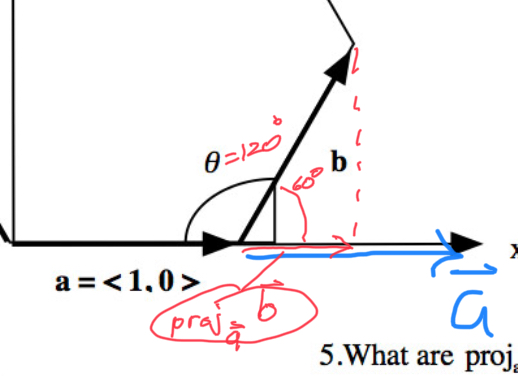
The projection of $\myv b$ onto $\myv a$ is a vector which has magnitude $b\cos 60^o=1*\frac12=$1/2, and points in the direction of $\myv a$. Now, the length of $\myv a$ is 1, so it is already a unit vector, so I could writes this as $\text{proj}_{\myv a}\myv b=\frac 12 \myv a$ or $\frac12 \uv a$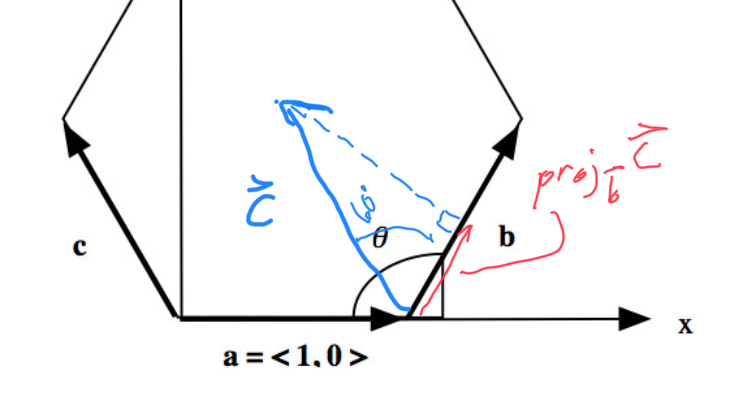
$\text{proj}_{\myv b}\myv c = $ $\frac 12\uv b$.
The component of a vector is a scalar. From the sketch, than answer is 1