9.6 - Staying Cool
Let $T(x,y)$ be the temperature in a 10 ft by 10 ft room on a winter night. One corner of the room is at (0,0) and the opposite corner is at (10,10). For both of the numbered functions, $T(x,y)$, answer these three questions:
- Draw, or describe in words, or plot with GeoGebra a graph of the temperature function. Useful prototype commands in GeoGebra: (This should plot one quadrant of a sphere)
function(sqrt(81-x^(2)-y^(2)), 0, 10, 0, 10)
z=4
The last four numbers are the $x$-range to plot, $0\lt x\lt 10$, and then the $y$-range to plot, also 0 to 10. The command z=4 will display the plane perpendicular to $\uv z$ at a height of $z=4$. This lets you easily see what part of the surface is above 4 and what part is below 4. <>Now, for each of the Temperature functions, $T(x,y)$ for this 10 by 10 foot room, plot $z=T(x,y)$. Use your plot to answer these questions:
- Describe the likely floor locations of the heating vents. Sketch the locations on a 10 by 10 square.
- Suppose you like to sleep with a temperature of 70${}^o$ or less. Where would you put your bed? Again, sketch locations on a square.
- $$T(x,y)=78-\frac{1}{10}\left[ x^2+(y-5)^2 \right]$$
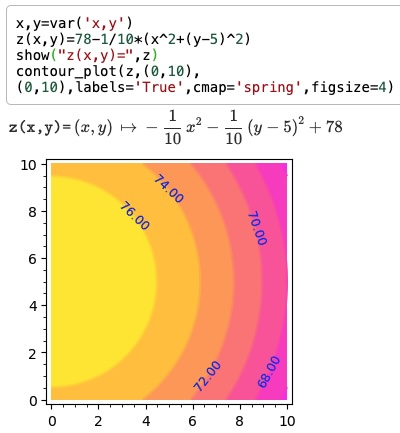
Heating vent in middle of left wall. Sleep below 70 (pink regions)
- $$T(x,y)=\frac12x-y+75$$
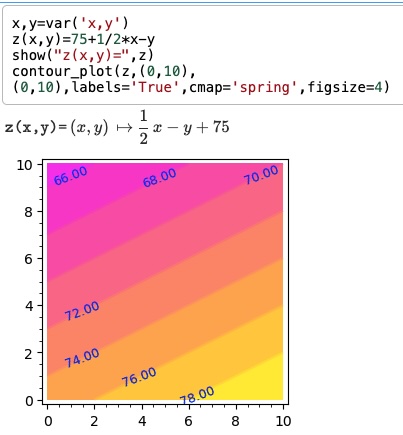
Heating vent along bottom, right corner. Sleep below 70 (pink areas)