[10.1] - Reading Assignment

After reading section 10.1...

1. This is a graph of the parametric curve $x(t)=\sin t$, $y(t)= |\cos (2t)|$, for $-\pi\lt t \lt \pi$.
   
   Write an equation of a position vector function, $\myv r(t)$ which describes the same curve. (This is not meant to be difficult!)

   $$\myv r(t)=\langle \sin t, |\cos(2t)|\rangle\ \ \ \text{for }-\pi \lt t \lt \pi, $$ or $$\myv r(t)=\sin t\,\uv i + |\cos(2t)|\,\uv j\ \ \ \text{for }-\pi \lt t \lt \pi.$$

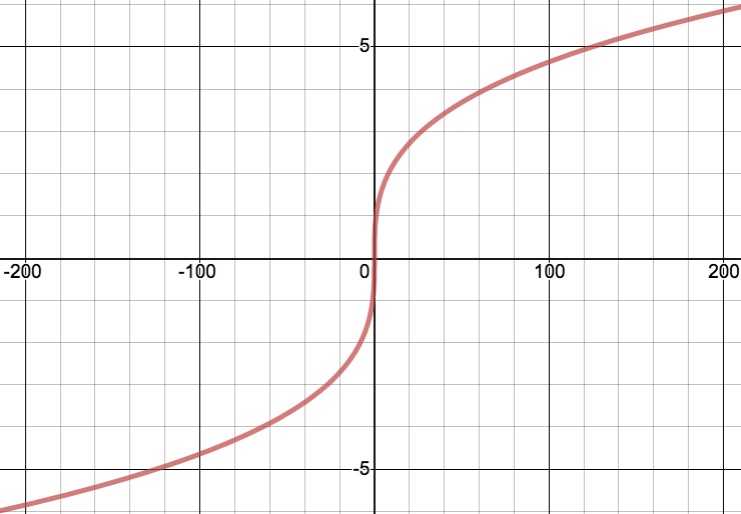
2. Sketch the curve described by the parametric, 2-d position vector function $(x,y)=\myc{t^3,t}$ where $t$ can take on any real value.

   Since $y=t$, we could write $x=t^3$ as $x=y^3$. So, think of $x$ as a function of $y$: $x(y)=y^3$, which looks like...
   

3. Muddy questions? Questions you wonder about?