Heat seeking kitten

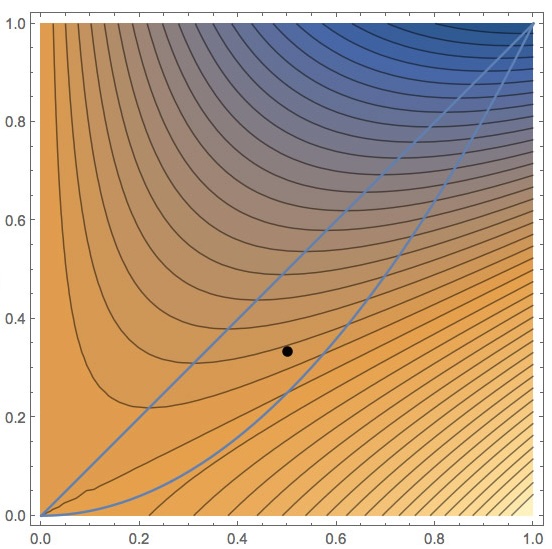Let $T(x,y)=x^2-2xy$ be the temperature at a point $(x,y)$ in the region bounded by the curves $y=x$ and $y=x^2$. (Blue lines on the accompanying contour plot.) Suppose that a kitten is crawling around the region.

1. At $P=(\frac12,\frac13)$ , in which direction should the cat go to cool down as quickly as possible?: Draw a vector on the contour plot indicating the direction. And find the components of the gradient and use it to justify your answer.
2. At $P$, in what direction(s) could the kitten go to maintain its current temperature?
3. Where is the hottest point inside the region? Mark it on the contour plot. Explain your answer.
4. If, at $P$, the cat moves in such a way that for each change in its $x$ direction of 2 units, the change in the $y$ direction is –1 unit, find a value for $\frac{dT}{dt}$, the rate of change of the temperature, from the kitten’s point of view. (Give your answer some plausible units).