11.6 - Bagels, bagels, bagels
See Tom Gauld's cartoon "...Torus never stopped feeling inferior...".
There are many ways to create bagels. Some people prefer boiling them, some prefer baking them, and some prefer defrosting then toasting them. Today we shall be creating bagels by the method of parameterizing them.
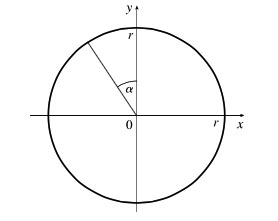
- Parameterize a circle of radius $2$ centered at the origin in the $xy$-plane starting at $(0, r)$. That is, find $x$, $y$, and $z$ in terms of $2$ and $\alpha$. Let $\alpha$ be the angle between the position vector and the $y$-axis.
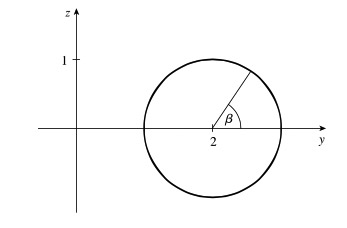
- Parameterize a circle of radius 1 in the $yz$-plane with center (2, 0) starting at (0, 3). Let $\beta$ be the angle between the position vector and the positive $y$-axis.
-
Now we want to characterize a typical point on our bagel,
so we can write a vector function $\myv r (\alpha, \beta)$ whose range is the entire breakfast treat. To find any specific point we
(a) Move $\alpha$ radians along the horizontal curve, then (b) Rotate $\beta$ radians along the vertical curve.
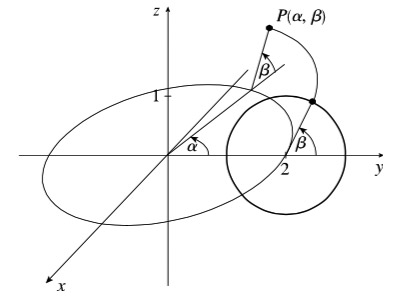
Find the coordinates of a point on the surface of the bagel parameterized by $\alpha\to u$ and $\beta\to v$. That is, find $x$, $y$, and $z$ functions, $$\myv r(\alpha, \beta)=\langle(x(\alpha,\beta), y(\alpha,\beta), z(\alpha,\beta)\rangle.$$ Then find limits on the parameters so that we can tell GeoGebra to plot a surface like... Surface( myx($u$,$v$), myy($u$,$v$),myz($u$,$v$), $u$, ___,___, $v$, ___,___) Find the three coordinate functions, and fill in the min and max limits of $\alpha\to u$ and $\beta\to v$.
[Here's Norm Prokup's Geogebra torus with major radius=5 and minor radius 2.]
My Geogebra one with major radius 3 and minor radius 2:
$$\myv r(u,v)=+(3+2\cos v)\cos u\,\uv x +(3+2\cos v)\sin u\,\uv y +2\sin v\,\uv x$$
From this, I can calculate the tangent vectors...
$$\myv r_u = \langle (3+2\cos v)(-\sin u), (3+2\cos v)\sin u), 0 \rangle$$
$$\myv r_v = \langle -2\sin v\cos u,-2\sin v\sin u, 2\cos v\rangle$$
To calculate the surface area...
- Calculate $\myv r_u$ and $\myv r_v$
- Notice that they are at right angles to each other!
- ...So, the magnitude $|\myv r_u\times\myv r_v|=|\myv r_u|*|\myv r_v|$