Space and Time [1.1, 1.2]

Space and Time

Readings: [1.1, 1.2] in Taylor, [vector algebra] in mathphys.

A particle

"A body whose dimensions may be neglected in describing its motion" (Landau and Lifshitz).

Might be an electron. Might be Saturn.

Positions & vectors

Vectors are terribly useful to keep track of the position of a particle. But remember that a vector is unique only for its direction and length, and not its position.

Underdog (early 1960s) from tvtropes So we use a particular kind of vector, a position vector to keep track of particle positions.

The vector $\myv{r}$ is referred to as a position vector when its:

base is at the origin of a coordinate system and
tip is at a point, the desired position.

Such a position vector of a particle can be represented in many ways (different notations but all the same unit vectors): $$\myv{r} = x \uv{i} + y \uv{j} + z \uv{k} = (x,y,z)=r_1 \uv{x} + r_2 \uv{y} +r_3 \uv{z} = r_1\uv{e}_1+r_2\uv{e}_2+ r_3\uv e_3=... $$

$\myv r$ is the conventional position vector. But $\myv r$:

does *not* refer to the radius of a circle
is *not* the same as the cylindrical coordinate $r$: which is just one component of the vector position.

Read this MathPhys topic on Vector Algebra...

Review sections from Calculus III on vectors and the dot product, to make sure you are ready to take full advantage of vector notation.

The length (or norm) of a vector $\myv{a}$ is written as $$a \equiv \sqrt{ \myv{a} \cdot{ \myv{a}}}\equiv | \myv{a} |.$$

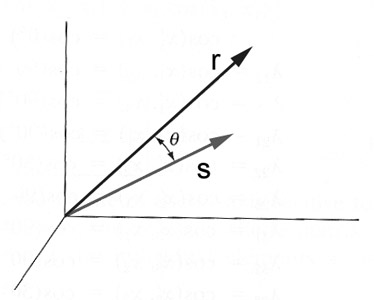The dot product (or 'scalar product') of two vectors is defined (in a way which is independent of the coordinate system) as $$\myv r \cdot \myv s=rs\cos\theta.$$

Does it matter which way we measure $\theta$, the angle between the two vectors? E.g. positive $\theta$ is defined as the angle between the first vector and the second, or vice versa? Does it matter if $\theta$ is measured "inside" or "outside" the two vectors?

Differentiation

This class is overwhelming concerned with motion: How a moving particle responds to forces and fields.

We'll use Newton's notation or "flyspeck" notation--the convention used in your textbook--where the time derivative of a function of time is denoted by a dot above the function... $$\dot z(t)\equiv \frac{d}{dt}z(t);\ \ \ddot z(t)\equiv \frac{d^2}{dt^2}z(t).$$

The velocity vector is the first derivative of position. Most generally, using the chain rule, that is: $$\begineq \myv{v} &\equiv& \dot{\myv r}\equiv \frac{d \myv{r}}{d t} =\frac{d}{dt} [x\uv i+y\uv j+z\uv k]\\ &=&\dot x\uv i+x\dot{\uv i} + \dot y\uv j+y\dot{\uv j} + \dot z\uv k+z\dot{\uv k} \endeq$$ ...seeing as how both the coordinates and the unit vectors could conceivably be changing as functions of time.

But for the Cartesian coordinate system (and neglecting relativity) the unit vectors are not changing with time/motion, so the time derivatives of the unit vectors vanish, and the expression above retains ony 3 of the terms above: $$\myv v = \dot{\myv r} =\dot x\uv i + \dot y\uv j + \dot z\uv k .$$ Which can also be written as $\myv v = v_x\,\uv x+v_y\,\uv y+v_z\,\uv z$. But we shall have occasion to deal with coordinate systems where the unit vectors are changing with time as well.

Generalized coordinates

For a collection of $N$ particles in 3-dimensional space, typically, $3N$ scalar numbers--coordinates--are needed to fully specify the locations of all the particles in space.

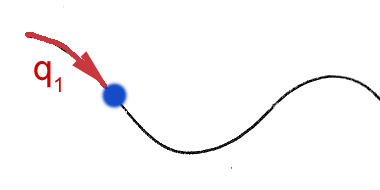Bead on a wire Yet, there are many dynamic systems which are constrained. The diagram suggests a bead sliding on a wire. If the equation of the wire in 3 dimensions is known, In this case it is possible to keep track of the position of the bead in space with just one coordinate, labelled $q_1$ and representing, in this case, the arc-length along the wire from some starting location. Knowing the equation traced out in space by the wire, the 3 spatial coordinates can be calculated from that arclenghth, that is: $$x=x(q_1);\ \ y=y(q_1);\ \ z=z(q_1);$$ The number of independent scalars $s$ needed to fully specify the positions is called the degrees of freedom, and those $s$ coordinates, $q_1, q_2,...q_s$ are the generalized coordinates, where $$s \leq 3N.$$

Deterministic system

We are interested in how a mechanical system changes in time. To calculate how a system changes we need not only the positions $q$ at some instant in time, but also the velocities $\dot{q}$. Landau and Lifshitz could write without qualification in 1960...

If all the coordinates and velocities are simultaneously specified, it is known from experience that the state of the system is completely determined, and that its subsequent motion can, in principle, be calculated.

This program works well for things like baseballs and rockets but chaotic motion, which we shall see occurs in some deceptively simple systems such as two connected pendulums, challenges this program.