Linear Momentum

In Chapter 1 we found a relationship between external forces and the total momentum of a system of many particles. $$\dot{ \myv{P} } = \sum_{\alpha} \myv{F} _{\alpha}^{ext} \equiv \myv{F} ^{ext} $$

• We get to decide what the "system" is: We can chose whichever particles we like.
• In the case that $\myv{F}^{ext}=0$, the momentum of the system is "conserved" (doesn't change with time).

The rocket problem

Here's a non-trivial momentum conservation problem:

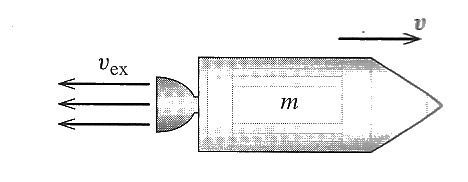
• A rocket in "outer space" with no external forces acting on it $\Rightarrow \myv P(t)= $ constant.
• Moving along a line (dispense with vector notation).
• The rocket can accelerate by means of "throwing back" fuel combustion products $\Rightarrow$ The mass of the rocket, $m(t)$, is changing with time. So is the rocket's speed, $v(t)$. "Shoe Power" - from Physics: Concepts and Connections by Art Hobson
• During a small time interval $dt$, the rocket's mass changes by a negative amount, $dm$, corresponding to the fuel it just threw out, so that the rate of change of the rocket mass is $\frac{dm}{dt}<0$.
• The fuel exhausted is travelling at speed $v_{ex}$ relative to the rocket--an accelerated reference frame. $v_{ex}$ is a positive number.
• Relative to a 'stationary' observer, the rocket exhaust appears to have speed $v-v_{ex}$ towards the right. (Or, as Taylor prefers, a speed $v_{ex}-v$ towards the left).

Consider the total momentum of the system of (rocket + fuel) at $t$ and a little later at $t+dt$:

$P(t)=m(t)v(t)=$ momentum of the rocket, including fuel that it has not yet ejected at $t$. $$\begineq P(t+dt)=&\text{momentum of lighter rocket - momentum of ejected fuel products}\\ =&(m+dm)(v+dv) - (-dm)(v_{ex} - v)\\ =&mv \color{red}{+ v\,dm}\color{black} +m\,dv + \color{blue}{dm\,dv}\color{black} \ \ \ + v_{ex}\,dm \color{red}{- v\,dm}\\ \approx& mv + m\,dv + v_{ex}\,dm \endeq $$

• The two red terms cancel to 0.
• The blue term is the product of 2 small differentials. This will be negligible compared to the remaining terms, some of which contain a single differential.

The total momentum is not changing (no external force) so we can set $P(t)=P(t+dt)$ and the equation becomes: $$0 = m\,dv + v_{ex}\,dm.$$

Separation of variables leads to... $$dv = -v_{ex}\frac{dm}{m}$$

Assuming that $v_{ex}$ is a constant, we can integrate this to find... $$v(t) - v_0 = -v_{ex} [\ln(m) - \ln (m_0)]= v_{ex} \ln(m_0/m(t))$$

In problem 12, you will find that you can get a bigger change in velocity by burning a set amount of fuel in stages, discarding empty tanks as you go, rather than all at one go: This can be made intuitively plausible by thinking about a two-stage rocket, and thinking about your choices after burning half of your fuel...

• NASA Mach 8 rocket sled documentary

Center of Mass

Consider a system of $N$ particles:

• Each particle is located at position $\myv{r}_\alpha$ with mass $m_\alpha$.
• The mass of the system is $M=\sum_{\alpha=1}^N m_\alpha$.

We can calculate the position vector pointing to the "center of mass" as an average of the positions of the particles, where each position is weighted by the mass fraction of the particle at that position: $$\myv{R} \equiv \sum_{\alpha=1}^N \frac{m_\alpha}{M} \myv{r}_\alpha =\frac{1}{M}\sum_{\alpha=1}^N m_\alpha \myv{r}_\alpha.$$

If the masses of the particles are constant: $$\dot{\myv{R}} = \frac{1}{M}\sum_{\alpha=1}^N m_{\alpha} \dot{\myv{r}}_\alpha = \frac{1}{M}\sum_{\alpha=1}^N m_\alpha\myv{v}_{\alpha} = \frac{1}{M}\sum_{\alpha=1}^N \myv{p}_{\alpha} =\frac{1}{M}\myv{P} .$$

Multiplying both sides of this equation by $M$ and taking the time derivative of both sides we get $\dot{ \myv{P} } = M \ddot{\myv{R}}$. And since we previously showed that $\myv{F}_{ext} =\dot{\myv{P}}$:

$$\myv{F}_{ext} = M\, \ddot{\myv{R}}.$$

This means that the center of mass, $\myv R$, of a collection of particles, moves as if it were:

• a single particle with the total mass $M$ of the system,
• subject to a single force $\myv F_{ext}$, which is the sum of the external forces acting on the system parts,
• which accelerates according to Newton's 2nd Law.

[Locating the CM / Rotating thingy demonstration, #1]

Continuous body

To find the CoM in a continuous body, we need to integrate to find the mass-fraction weighted average of the positions of many infinitesimal "chunks" of mass, $dm$, at positions $\myv r$. We could write this in terms of a continuously varying mass density function, $\myv \rho(\myv R)$, and a chunk of volume instead using $dm=\rho(\myv r)\,dV$:

$$\myv{R} =\frac{1}{M}\int \myv{r} \,dm = \frac{1}{M} \int\rho(\myv{r}) \myv{r}\,dV$$

Angular momentum

The angular momentum of a particle relative to the origin is: $$\myv{\ell} = \myv{r} \times \myv{p}.$$

Consider a particle of mass $m$ moving along a straight line at constant speed, $v$ (and therefore with constant linear momentum). Consider some arbitrary reference point, $P$, in space, such that the particle's trajectory passes within a distance $a$ of $P$ at its closest approach. Calculate the particle's angular momentum relative to $P$ at some convenient point in time, and show that this angular momentum is unchanging no matter where the particle is along its trajectory.

The time rate of change of angular momentum... $$\dot{\myv{\ell}} = (\dot{\myv{r}} \times \myv{p}) + (\myv{r} \times \dot{\myv{p}}) =m (\dot{\myv{r}} \times \dot{\myv{r}}) + (\myv{r} \times \myv{F}) \equiv \myv{\Gamma}$$

is the Torque $\myv{\Gamma}=\myv r \times \myv F$. I've used that property that for any vector, $\myv{b}\times\myv{b}=0$.

Angular momentum for several particles

For $N$ particles, each with angular momentum $\myv{\ell}_\alpha = \myv{r}_\alpha \times \myv{p}_\alpha$ $$\myv{L} = \sum_{\alpha=1}^N \myv{\ell}_\alpha = \sum_{\alpha=1}^N \myv{r}_\alpha \times \myv{p}_\alpha.$$

In analogy with our results for linear momentum, if we separate the forces acting on our $N$ particles into internal and external forces, and if we once more assume that the internal forces are central it is possible to show: $$\dot{\myv{L}} = \myv{\Gamma}^{ext}$$

One particular case: If the sum of external torques adds up to zero, then the total angular momentum is conserved.

It's not at all obvious, but we'll find later that, if you take as the origin the center of mass (COM), that, with no external torques, $\myv{L}_{COM}$ is conserved even if the COM is being accelerated.

[Rotating thingy demonstration!]

Moment of Inertia

Recall that in General Physics you also talked about a Moment of Inertia, $I$, such that the angular momentum about, say, the $z$-axis is $L_z = I \omega$ and you calculate it like: $$I = \sum m_\alpha d_\alpha^2$$

Where $d_\alpha$ is the distance from the axis of rotation of mass $m_\alpha$.

Problem 3.31

Use the equation above to calculate the moment of inertia of a uniform disk of mass $M$ and radius $R$ rotating about its axis. Turn the sum into an integral and carry it out in cylindrical coordinates.

[In Cartesian coordinates, $dV=dx\,dy\,dz$. In Calc III we figured out how to express $dV$ in other coordinate systems.

Example 3.4 - Dumbbell

Movies

Homework

Chapter 3: 4, 10, 12, 17, 25