Thevenin-equivalent circuits

Linear circuit elements

Linear means voltage, $V$, is a linear function of current (or vice versa)

Resistor

$R$ is a constant.$$V=IR$$

Battery or power supply

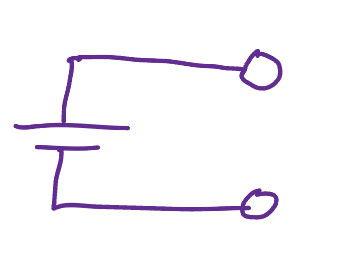An ideal battery maintains a constant voltage and can supply any current as necessary to keep the same voltage. (*) A real battery has some limit on the current.
$$V=\text{constant}$$

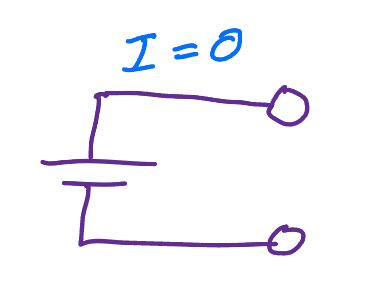
Current source

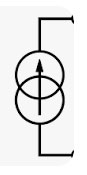An ideal current source maintains a constant current and can supply any voltage necessary to keep the same same current flowing. (*) A real current source has some limit on the voltage.
$$I=\text{constant}$$

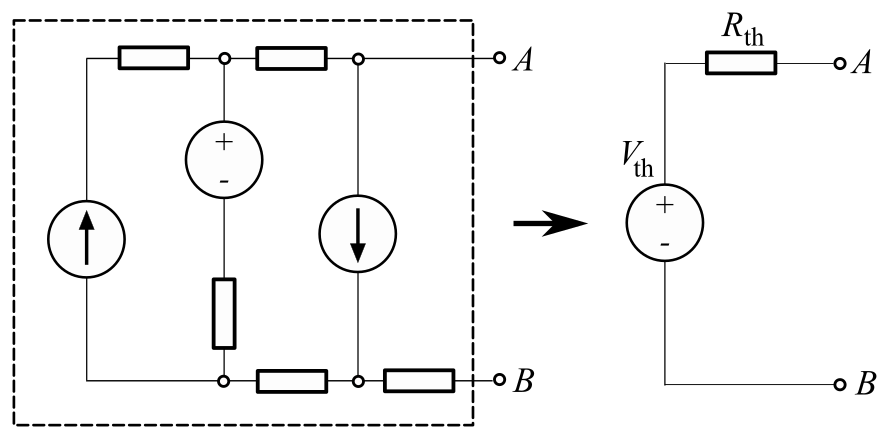
Thévenin's theorem

Any black box circuit of resistors, batteries, and current sources is indistinguishable to the outside world from its Thevenin equivalent circuit consisting of a single voltage source in series with a single resistor.

By Svjo, Wikimedia Commons - Own work, CC BY-SA 4.0

• Video and Examples at circuitbread.com.

Finding $V_\text{th}$ and $R_\text{th}$

To find the equivalent Thevenin voltage and resistance:

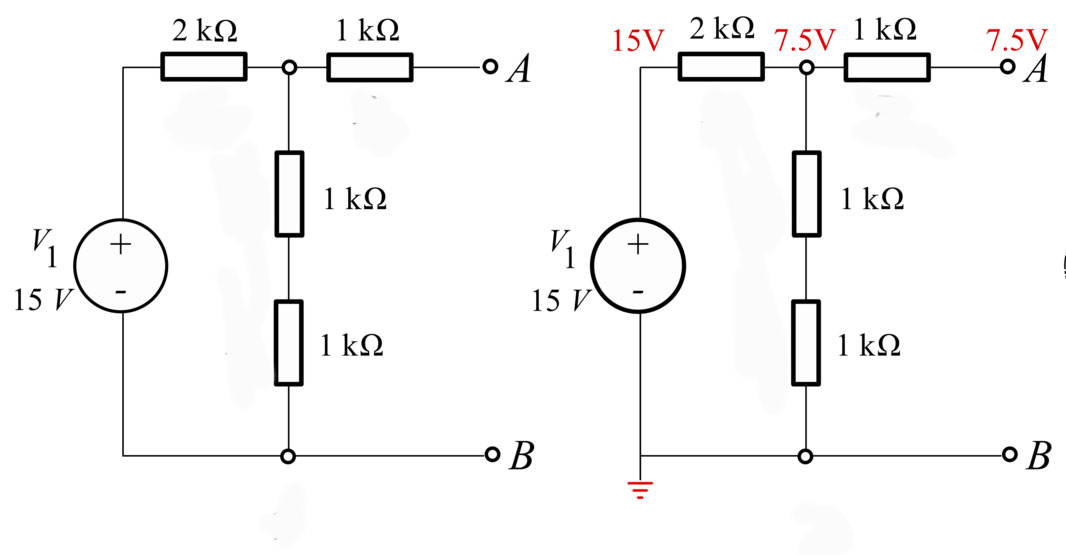
• $V_\text{th}$ is the open circuit voltage between the output terminals.
  
  
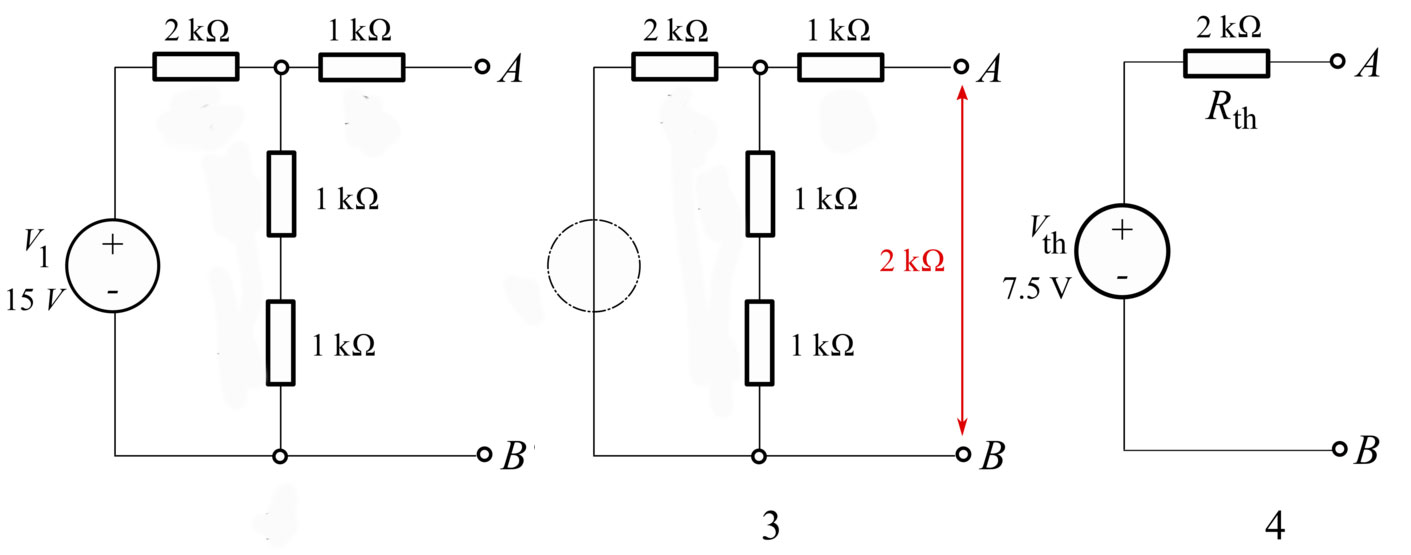
• To find $R_\text{th}$
  • Replace all batteries with wires,
  • Cut all constant circuit sources out of the circuit (leaving a gap),
  • and Calculate the equivalent resistance across the output terminals.

  
  

• Alternately, you could connect $A$ to $B$ (short circuit the outputs) and measure the short-circuit current $I_\text s$. Work backwards to find $R_\text{th}$ as... $$R_\text{th}=V_\text{th}/I_\text s.$$

  Meaning of $V_\text{th}$ and $R_\text{th}$

  • $V_\text{th}$ is the resting or 'natural' output that the circuit "wants" to be at.
  • $1/R_\text{th}$ is a measure of how 'stiff' the circuit: The stiffer the circuit the greater the current needed to lower the voltage appreciably.