The finite square well

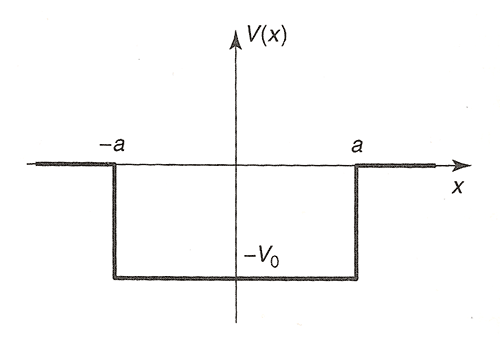
$$V(x)=\left\{ \begin{array}{ll} -V_0 &\ \ \ |x| \leq a\\0 &\ \ \ |x|\gt a \end{array} \right. $$ This potential should have both bound ($-V_0\lt E\lt 0$) and scattering ($0\lt E$) states:

Bound states: $E\lt 0$

In the two regions $|x|\gt a$, $V(x)=0$, so Schrödinger says: $$-\frac{\hbar^2}{2m}\frac{d^2\varphi}{dx^2} =E\varphi\ \ \text{or }\frac{d^2\varphi}{dx^2}=\kappa^2 \varphi,$$ where $\kappa=\sqrt{-2mE}/\hbar$ is real and positive. There are two solutions in each region, but to make sure that $\varphi(x)\to 0$ as $x\to \pm\infty$, we will have: $$\varphi(x)=\left\{\begin{array}{ll} Be^{\kappa x} &\ \ \ x \lt -a\\ Fe^{-\kappa x} &\ \ \ a \lt x \end{array}\right.$$

In the well $|x|\leq a$, $V(x)=-V_0$, so Schrödinger says: $$-\frac{\hbar^2}{2m}\frac{d^2\varphi}{dx^2}-V_0\varphi =E\varphi\ \ \text{or }\frac{d^2\varphi}{dx^2}=-l^2 \varphi,$$ where $l=\sqrt{2m(E+V_0)}/\hbar$ is real and positive. There are two solutions and we'll write the general solution as a superposition of the form: $$\varphi(x)=C\sin lx + D\cos lx.$$

Taking advantage of the symmetry (the potential well is even) we'll work with the half-well potential

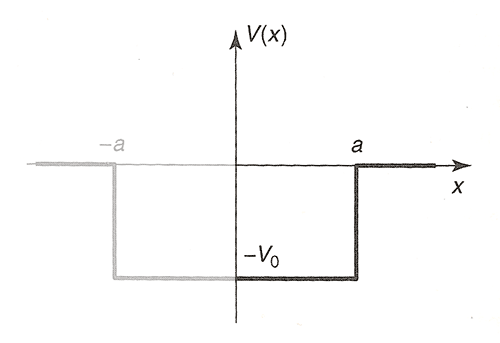
and look for even solutions where $\varphi(-x)=\varphi(x)$. [I'll leave the odd ones for you...]

The even solutions in the well are the ones where $C=0$ and $\varphi(x)=D\cos lx$.

Applying the boundary conditions...

Continuity of the wave function $\varphi(x)$ at $x=a$: $$Fe^{-\kappa a}=D\cos la.$$

Continuity of the slope, $\varphi'(x)$ at $x=a$: $$-\kappa Fe^{-\kappa a}=-l D\sin la.$$

Dividing the two equations: $$\kappa = l \tan la,$$

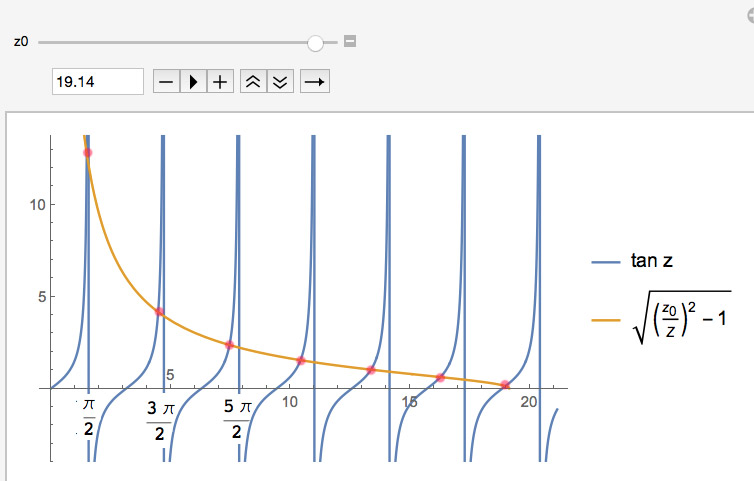
and re-arranging: $$\begineq \frac{\kappa }{l} &= \tan la \\ \sqrt{\frac{-2mE/\hbar^2}{2m(E+V_0)/\hbar^2}} &= \tan\left( \sqrt{2mE+V_0}a/\hbar\right)\\ \sqrt{\frac{2mV_0-2m(E+V_0)}{2m(E+V_0)}} &= \tan\left( \sqrt{2mE+V_0}a/\hbar\right)\\ \sqrt{(z_0/z)^2-1} &= \tan z\\ \endeq $$ where $z=\sqrt{2m(E+V_0)}\frac a\hbar$ and $z_0=\sqrt{2mV_0}\frac a\hbar$. This is a transcendental equation in one variable, $z$.

For bound states, $E \lt 0$ and we know there are no solutions when the energy is below the bottom of the well. $E+V_0$ is the energy of the state above the bottom of the well:
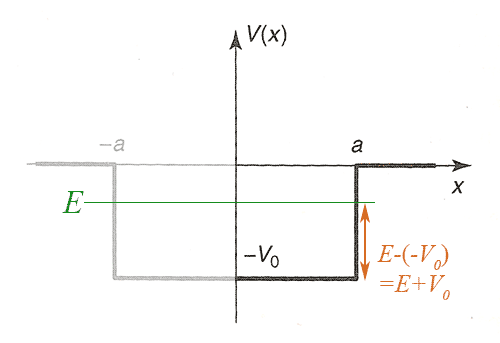
The ratio $$(z_0/z)^2=\frac{V_0}{E+V_0}$$ is always greater than one.

Increasing $z_0=\sqrt{2mV_0}a/\hbar$ corresponds to a deeper and/or wider well.

[Graphical solution of $\sqrt{(z_0/z)^2-1} = \tan z$.]

The graph of $g(z)=\sqrt{(z_0/z)^2-1}$ is 0 when $z=z_0$.

A couple things to notice:

• $z_0\to 0 \equiv$ (shallow / wide well):

  It would appear that there is always at least one even, bound state, even for a vanishingly shallow well.
  

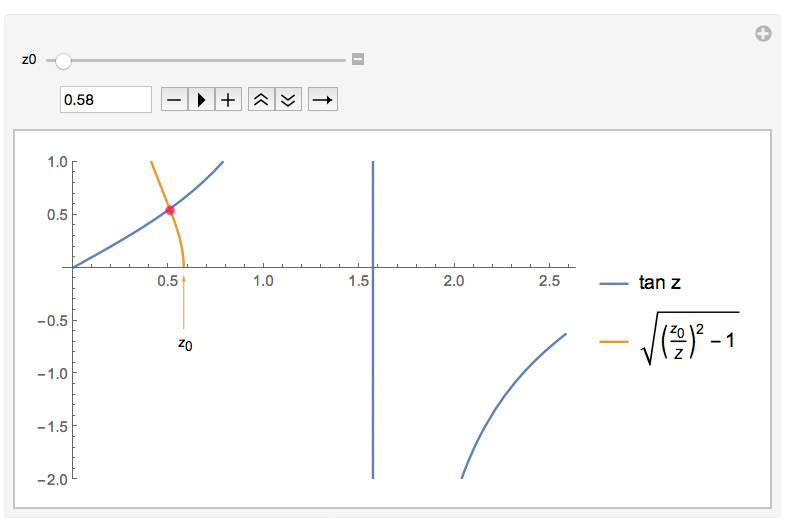
• $z_0\to \text{large} \equiv$ (deep / narrow well):

  The solutions (particularly for the states close to the ground state) are very close to, but less than the vertical lines at $$z=\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},\frac{7\pi}{2},...$$ or $z_n=n\pi/2$ for odd values of $n$.

  Since $z\equiv la=\frac{\sqrt{2m(E+V_0)}}{\hbar}a$ this implies $$E_n+V_0\approx \frac{n^2 \pi^2 \hbar^2}{2ma(2a)^2}=E_{\infty n}$$ That is, the solutions have energies(*) which are approximately equal to(**) the energies(***) of the stationary states of the infinite square well(****).

  !!

  * $E+V_0$ is the energy of a state above the bottom of the finite square well.
  ** but slightly less than,
  *** with $n$ odd.
  **** the infinite square well of width $2a$.
  

Homework