Addition of angular momenta

Adding angular momenta

Classical angular momentum

Classically, the total angular momentum of any collection of particles, each with its own momentum is: $$\myv L=\sum_i\myv r_i\times\myv p_i.$$

We can write $\myv r_i=\myv R_{cm}+\myv r'_i$ in terms of the position of the center of mass. Then it turns out we can separate the sum for the total angular momentum into two pieces: $$\myv L= \myv R_{cm}\times\myv P_{cm} + \sum_i \myv r'_i\times \myv p_i.$$ The second term is what we mean by "spin": angular momentum about the center of mass of a body.

If the center of mass is not moving, then we have: $$\myv L = \myv S.$$

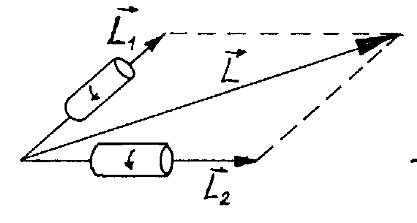
If the collection of particles can be grouped into two objects, each with its own local center of mass, and each of the centers of mass is unmoving, then the total angular momentum is just: $$\myv L = \myv L_1 +\myv L_2.$$

Depending on the angle between the two object's angular momenta, we'd expect that the total angular momentum $L=|\myv L|$ should be somewhere between: $$|L_1-L_2| \leq L \leq L_1 + L_2.$$ Can we also usefully talk about the total angular momentum in QM? Yes!

Total angular momentum in QM

The proton is a spin 1/2 particle, with the same magnitude of spin as the electron.

Consider a hydrogen atom in its ground state--so that the orbital angular momentum of the electron relative to the proton is 0. Now we only have to worry about contributions to the total angular momentum of the two spins, and not their mutual angular momentum.

What is the angular momentum of this composite system of two spin-1/2 particles? In analogy with classical mechanics, it out to be (in terms of operators): $$\hat{\myv S}=\hat{\myv S}^e+\hat{\myv S}^p.$$ We've never dealt with $\hat{\myv S}$ of even one particle directly up until now: We've managed to work only in terms of the total angular momentum squared $\hat S^2$ and one component of the spin at a time, e.g. $\hat S_z$. We'll do the same sort of thing in what follows.

The $z$-component of each particle's spin can take on the values $+\hbar/2$ or $-\hbar/2$.

Seeing as these are distinguishable particles, measuring the $z$-component of one particle should not impact the measurement of the $z$-component of the other. We could assemble a basis in terms of the two possible $\hat S_z$ eigenstates of each particle (written with the proton spin state first, then the electron): $$\chi = \ket{\frac{1}{2}m^p}\ket{\frac{1}{2}m^e} = \chi^p \chi^e.$$

Here, $p$ and $e$ are indices indicating which particle the operator works on--not powers.

The four states are $$\ket{\uparrow\uparrow}, \ket{\uparrow\downarrow}, \ket{\downarrow\uparrow}, \ket{\downarrow\downarrow}.$$

Since we assumed that the $H$ atom was in its ground state (total orbital angular momentum quantum number $l=0$), only the angular momentum of the spins of the electron and proton contribute to the total angular momentum of this two-particle system.

To motivate what comes next...

Each particle can be in a spin up or spin down state (two eigenstates each of the single particle operators $\hat S_z^e$ and $\hat S_z^p$),
and so there are four possible combinations.
From what we know about QM, these states must "span the space" of all possible two particle states. That is any state of this system should be expressable as some linear combination of these four basis states: $$\ket\Psi = a\ket{\uparrow\uparrow} + b\ket{\uparrow\downarrow} + c\ket{\downarrow\uparrow} + d\ket{\downarrow\downarrow}.$$
Now, we could ask if there are eigenfunctions of the total angular momentum operator $\hat S^2$ and the operator $S_z$ for the $z-$component of the total angular momentum of the two-particle system?
If so, these eigenfunctions should be expressable as a linear combination of the single-particle eigenstates.

We're interested in things having to do with $\myv{S}=\myv{S}^p+\myv{S}^e$.

The operator for $z$-component of total system angular momentum should be $$ \hat S_z = \hat S_z^p+\hat S_z^e.$$

For example: What is the $z$-component of the compound spin state $\ket{\uparrow \downarrow}$? $$\begin{eqnarray}(\hat S_z^p+\hat S_z^e) \ket{\uparrow \downarrow} & = & (\hat S_z^p\chi_+^p)\chi_-^e +\chi_+^p (\hat S_z^e \chi_-^e) \\ & = & (\frac{\hbar}{2}\chi_+^p)\chi_-^e +\chi_+^p (-\frac{\hbar}{2}\chi_-^e) \\ & = &(\frac{\hbar}{2} - \frac{\hbar}{2}) \chi_+^p\chi_-^e \\ & = & 0. \end{eqnarray} $$

Hmmm, there are states with $\hat S_z=-1, 0,0,1$. It seems like the total angular momentum quantum number should be $s=1$, but what about the two $m=0$ states?

Surely the state $\ket{\uparrow \uparrow}$ with $m = 1\hbar$ belongs to the total angular momentum state with $s=1$. That is, in terms of the total angular momentum $\hat S^2$ and total $\hat S_z$ quantum numbers, $\ket{s=1,m=1} \equiv \ket{11}=\ket{\uparrow \uparrow}$. Now, apply the operator $\hat S_- = \hat S_-^p+\hat S_-^e$ to this state: $$ \begin{eqnarray} \hat S_-\ket{\uparrow \uparrow} & = & (\hat S_-^p+\hat S_-^e)\chi_+^p\chi_+^e \\ & = & (\hat S_-^p\chi_+^p)\chi_+^e + \chi_+^p(\hat S_-^e \chi_+^e) \\ & = & (\hbar \chi_-^p)\chi_+^e + \chi_+^p(\hbar\chi_-^e) \\ \hbar\sqrt{2}\ket{10} & = & \hbar(\ket{\downarrow \uparrow} + \ket{\uparrow \downarrow}) \end{eqnarray} $$

where we've used our norm equation for the raising / lowering operators, to write $\hat S_-\ket{11}=\hbar\sqrt{2}\ket{10}$.

It seems like it would be a good guess that there are three related states--a "triplet" of states--with total spin $s=1$--that we get when successively applying $\hat S_-$ to $\ket{11}.$: $$\ket{11} = \ket{\uparrow \uparrow},$$ $$\ket{10} = \frac{1}{\sqrt{2}}(\ket{\uparrow \downarrow} + \ket{\downarrow \uparrow}),$$ $$\ket{1-1} = \ket{\downarrow \downarrow},$$

We can still construct one more state which is orthogonal to all the states above, with a total angular momentum $z-$component of 0: $$\frac{1}{\sqrt{2}}(\ket{\uparrow \downarrow} - \ket{\downarrow \uparrow})\stackrel{?}{\equiv}\ket{00}.$$ Hopefully this is the remaining eigenstate of the total angular momentum operator that has $s=0$.

Certainly these states have the right eigenvalues for the $\hat S_z$ operator. But to really nail these identifications, we need to show that these are eigenstates of $\hat S^2$ with the expected eigenvalues.That is, we should find $$\hat S^2\ket{10}=s(s+1)\hbar\ket{10}=1(2)\hbar\ket{10}=2\hbar\ket{10},$$ and $$\hat S^2\ket{00}=s(s+1)\hbar\ket{00}=0(1)\hbar\ket{00}=0.$$ So, we need to figure out how to represent...

The total angular momentum operator

$$\begin{eqnarray} \hat S^2 & = & (\myv{\hat S}^p + \myv{\hat S}^e)\cdot (\myv{\hat S}^p + \myv{\hat S}^e)\\ & = & (\hat S^p)^2 + (\hat S^e)^2 +2 \myv{\hat S}^p\cdot\myv{\hat S}^e\\ & = & (\hat S^p)^2 + (\hat S^e)^2 +2 (\hat S_x^p\hat S_x^e+\hat S_y^p\hat S_y^e+\hat S_z^p\hat S_z^e) \\ \end{eqnarray}$$

Let's let $\hat S^2$ operate on our supposed $\ket{10}$ state. Taking various pieces of this one at a time...

$$\begin{eqnarray} (\hat S^p)^2\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & \frac{1}{\sqrt{2}}\[((\hat S^p)^2\uparrow)\downarrow +((\hat S^p)^2\downarrow)\uparrow \]\\ & = & \frac{1}{\sqrt{2}}\[ \hbar^2 \frac{3}{4} \uparrow\downarrow + \hbar^2\frac{3}{4}\downarrow\uparrow \]\\ & = & \hbar^2\frac{3}{4} \frac{1}{\sqrt{2}}\[\uparrow\downarrow + \downarrow\uparrow \] \end{eqnarray}$$

Where we've used the fact that, when it's operating on a spin 1/2 proton state, the $(\hat S^p)^2$ operator yields $(\hat S^p)^2\ket{\uparrow^p} = s^p(s^p+1)\hbar^2\ket{\uparrow^p}=\frac{1}{2}\frac{3}{2}\hbar^2\ket{\uparrow^p}$.

Carrying out the same sort of operation with the $(\hat S^e)^2$ operator gives: $$\begin{eqnarray} (\hat S^e)^2\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & \hbar^2\frac{3}{4} \frac{1}{\sqrt{2}}\[\uparrow\downarrow + \downarrow\uparrow \] \end{eqnarray}$$

Consider $\hat S_x\ket{\uparrow}$: $$\hat S_x\ket{\uparrow} = \frac{\hbar}{2}\begincv 0 & 1\\1 & 0\endcv \begincv 1 \\ 0 \endcv = \frac{\hbar}{2}\begincv 0 \\ 1 \endcv = \frac{\hbar}{2}\ket{\downarrow}$$

We could also work out $\hat S_x\ket{\downarrow}=\frac{\hbar}{2}\ket{\uparrow}$. So, $$\begin{eqnarray} 2(\hat S_x^p\hat S_x^e)\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & 2\frac{1}{\sqrt{2}} \[((\hat S_x^p)\uparrow)(\hat S_x^e\downarrow) +((\hat S_x^p)\downarrow)(\hat S_x^e\uparrow) \]\\ & = & 2\frac{\hbar^2}{4}\frac{1}{\sqrt{2}} \[\downarrow \uparrow +\uparrow \downarrow \]\\ & = & \hbar^2\frac{1}{2}\frac{1}{\sqrt{2}} \[\uparrow \downarrow +\downarrow \uparrow \] \end{eqnarray}$$ It turns out that $\hat S_y\ket{\uparrow} = i\frac{\hbar}{2}\ket{\downarrow}$ and $\hat S_y\ket{\downarrow} = -i\frac{\hbar}{2}\ket{\uparrow}$, and so: $$\begin{eqnarray} 2(\hat S_y^p\hat S_y^e)\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & 2\frac{1}{\sqrt{2}} \[((\hat S_y^p)\uparrow)(\hat S_y^e\downarrow) +((\hat S_y^p)\downarrow)(\hat S_y^e\uparrow) \]\\ & = & 2\frac{\hbar^2}{4}\frac{1}{\sqrt{2}} \[(i)(-i)\downarrow \uparrow +(-i)(i)\uparrow \downarrow \]\\ & = & \hbar^2\frac{1}{2}\frac{1}{\sqrt{2}} \[\uparrow \downarrow +\downarrow \uparrow \] \end{eqnarray}$$ Finally, if we work out $\hat S_z\ket{\uparrow} = \frac{\hbar}{2}\ket{\uparrow}$ and $\hat S_z\ket{\downarrow} = -\frac{\hbar}{2}\ket{\downarrow}$, and so: $$\begin{eqnarray} 2(\hat S_z^p\hat S_z^e)\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & 2\frac{1}{\sqrt{2}} \[((\hat S_z^p)\uparrow)(\hat S_z^e\downarrow) +((\hat S_z^p)\downarrow)(\hat S_z^e\uparrow) \]\\ & = & \hbar^2\frac{1}{2}\frac{1}{\sqrt{2}} \[\uparrow (-1)\downarrow +(-1)\downarrow \uparrow \] \\ & = & -\hbar^2\frac{1}{2}\frac{1}{\sqrt{2}} \[\uparrow \downarrow +\downarrow \uparrow \] \end{eqnarray}$$

[deep breath]

Now we have the 5 pieces we need to put together... $$\begin{eqnarray} (\hat S)^2\frac{1}{\sqrt{2}}\[ \uparrow\downarrow + \downarrow\uparrow\] & = & \hbar^2$\frac{3}{4} + \frac{3}{4} + \frac{1}{2} + \frac{1}{2} - \frac{1}{2} $\frac{1}{\sqrt{2}}\[\uparrow\downarrow +\downarrow\uparrow \]\\ & = & \hbar^2$2$\frac{1}{\sqrt{2}}\[\uparrow\downarrow +\downarrow\uparrow \] \end{eqnarray}$$

This is precisely what we hoped for. We had expected that if $\frac{1}{\sqrt{2}}\[\uparrow\downarrow +\downarrow\uparrow \] = \ket{10}$, then applying the $\hat S^2$ operator we should get: $$\hat S^2\ket{10}=s(s+1)\hbar\ket{10}=1(2)\hbar\ket{10}=2\hbar\ket{10}.$$

By a similar method, we can show that $$\hat S^2\frac{1}{\sqrt{2}}\[\uparrow\downarrow -\downarrow\uparrow \] = 0,$$

and so we conclude that $\frac{1}{\sqrt{2}}\[\uparrow\downarrow - \downarrow\uparrow \] =\ket{00}$.

So, a different set of basis states we could use to describe this two-particle system, is the three triplet states, and the singlet state...

The singlet state

Let's say that you have somehow prepared this hydrogen atom in what you *know* is a singlet state. $$\frac{1}{\sqrt{2}}\[\uparrow\downarrow - \downarrow\uparrow \] =\ket{00}.$$

1.) What are the probabilities of different outcomes if you measured the $z$-component of the proton's spin? The $z$-component of the electron's spin?

2.) What would you get for the expectation value of the product of these two operators: $$\langle \hat S_z^p \hat S_z^e\rangle = ??.$$