3-dimensional coordinate systems [9.1]
Locating objects in 3-dimensions.

- Right-handed Cartesian coordinates
- Points in 3-D space
- Equations of planes
- Distance formula in 3 dimensions
- Equations of spheres
Rectangular coordinates
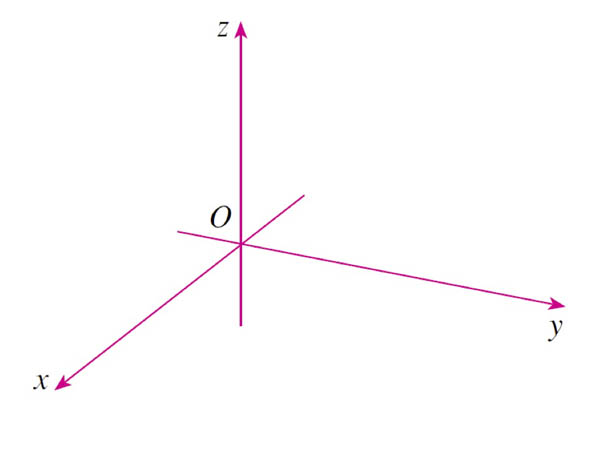
Also known as Cartesian coordinates, after Renes Descartes
Right-handed coordinate system
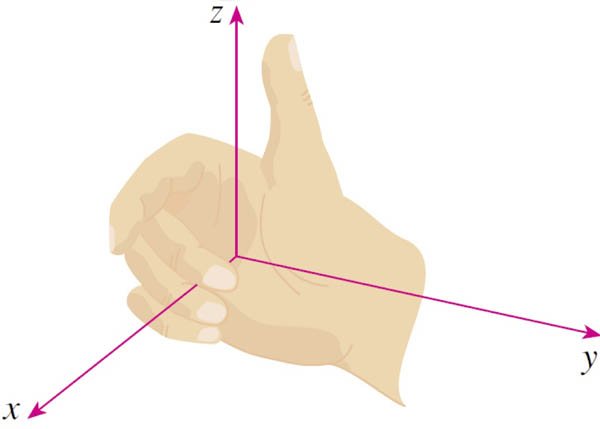
- Take your right hand...
- Point your straight fingers in the $\hat x$ direction.
- Rotate your hand so that you can curl your fingers* to point in the $\hat y$ direction.
- Your thumb now points in the $\hat z$ direction.
* You need to be able to curl your fingers through an angle less than $180^o$.
Try x and y, then x and z and y and z, and figure out which way the other axis points.
To Do
- Create a set of coordinate axes [pipecleaners]
- Do the Visualizing the xyz coordinate system worksheet (See the "handouts" folder):
Write down which color is your $x$-axis, your $y$-axis, and your $z$-axis.
Coordinate planes
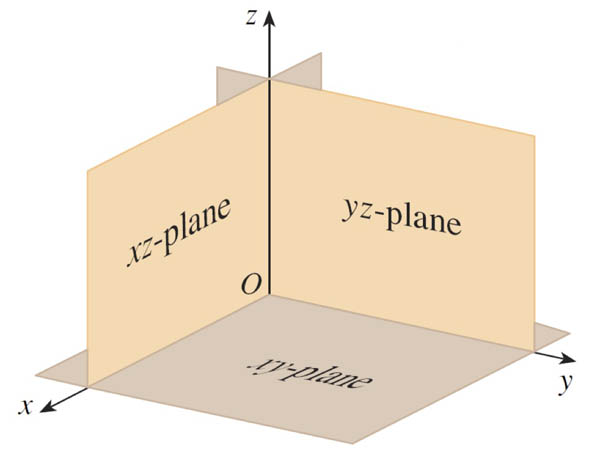
Coordinates
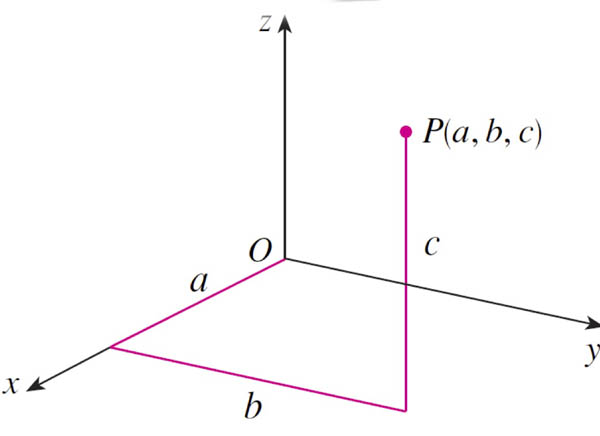
Projections
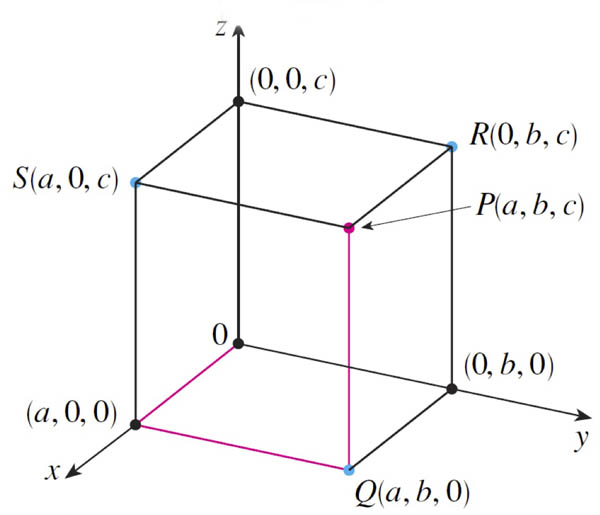
$S$ is the projection of $P$ onto the $xz$ plane.
$(0,b,0)$ is the projection of $P$ onto the $y$-axis.
The space $\mathbb{R}^3$
$\mathbb{R}\equiv$ the real numbers.
- Cartesian Product:
$\mathbb{R}^3\equiv \mathbb{R}\times\mathbb{R}\times\mathbb{R}=\{(x,y,z) | x,y,z\in \mathbb{R}\}$. - Set of all ordered triples.
To Do
- Points in the xyz coordinate system worksheet
Surfaces in $\mathbb{R}^3$
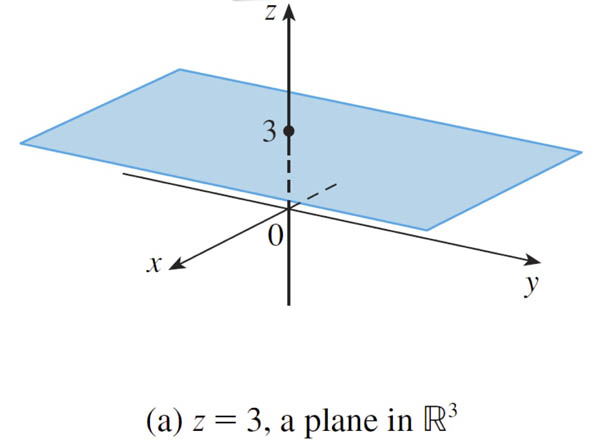
All points with coordinates $(a,b,c)$ where $c=3$
[and $a$ and $b$ can be anything]
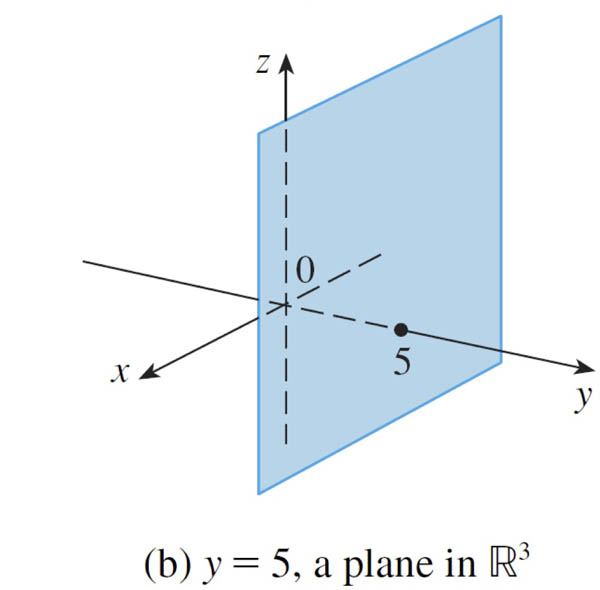
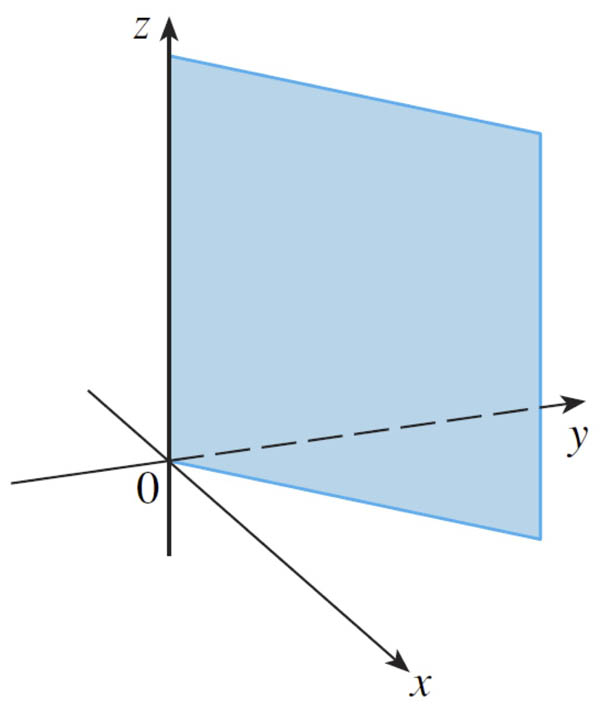
All points with coordinates $(x,y,z)$ where $y=x$.
Notice that $y=x$ is the definition of a line in 2-d with a slope of 1. But here??
Anything a bit deceptive about the picture above?
Should continue to values with x and y less than 0...
To Do
- Section 9.1 Group Work: Fun with Visualization [missing]
- Working with surfaces in 3D space [missing]
Distance
What is the distance $|P_1P_2|$ between two points $P_1(x_1,y_1,z_1)$ and $P_2(x_2,y_2,z_2)$ in three dimensional space?
With $\Delta x=x_2-x_1$, etc, you can imagine applying Pythagoras' theorem twice [at GeoGebra, 9.1.distance.nb]:
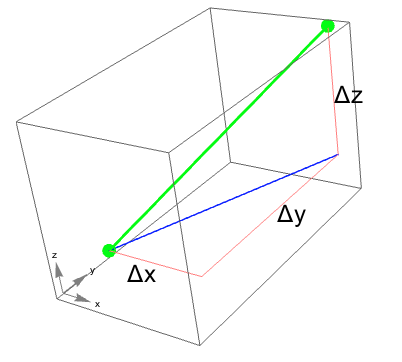
- The blue line is the hypotenuse of the triangle with legs $\Delta x$ and $\Delta y$: It's length is $\sqrt{(\Delta x)^2+(\Delta y)^2}$.
- The green line is our distance, and is the hypotenuse of the right triangle with legs of $\Delta z$ and the blue line.
So, our distance formula is: $$|P_1P_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}.$$
Equation of a sphere
All the points on a sphere are the same distance, $r$, away from its center, $C(h,k,l)$. Using the distance formula: $$(x-h)^2+(y-k)^2+(z-l)^2 = r^2.$$
These equations describe sets of points,$\{(x,y,z)\}$ that fulfill the equation equation. For each equation, make a guess at the surface corresponding to the equation, then check it by typing the equation into GeoGebra: [Hint, think about what the distance formula implies.]
- $$ 9=x^2+y^2+z^2.$$
- $$z=\sqrt{ 9-x^2-y^2}.$$
- $$9=x^2+y^2.$$
Problem 9.1.038
Consider a 2-d variation of this problem...Find all the points, $P$, (they form a circle) that are twice as far from $A$ as they are from $B$.
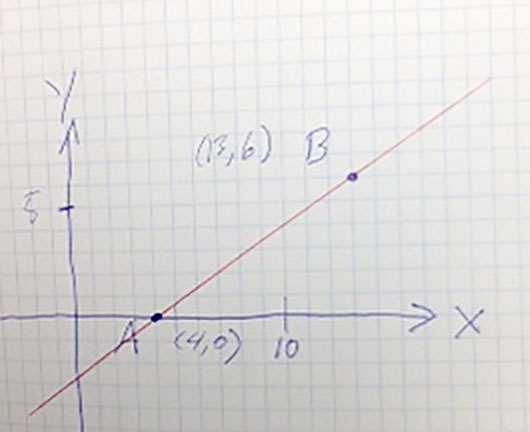
Well... It ought to be possible to find *some* of the points $P$. Consider these (leading) questions:
- How would you find the coordinates of a point which is halfway between $A$ and $B$?
- One of the points in the set $\{P\}$ should be on the line segment between $A$ and $B$. What fraction of the distance from $A$ to $B$ is that point?
- What are the coordinates of that point?
- There is one other point in $\{P\}$ along the red line, but not between $A$ and $B$. What fractional distance would it be? That is... if the distance from $A$ to $B$ were 1, what would the distance from $A$ to this second point be?
- Now we have a segment of the red line that connects two points on a circle. Either the line segment is a diameter line, or it is not. Can you make an argument for why the center of the circle could, or could not be away from the line segment?
- So, where is the center of the circle? And what is its radius?
Image credits