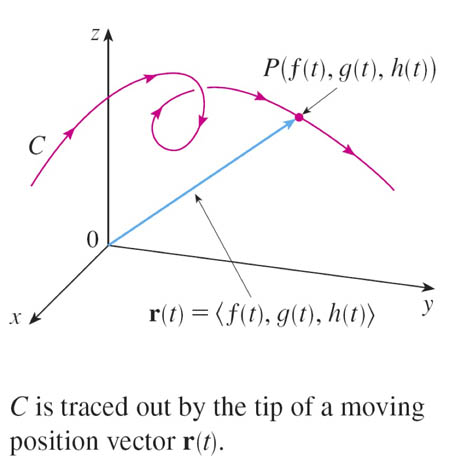
Vector functions [10.1]

Blessing of the media, Soyuz launch 2013 [NASA]

The position of an object in 3-d, as a function of time, $\myv r(t)$ is an example of a vector function.

Vector functions and parametric equations

Consider the 2-d vector function: $$\myv r(t)=\langle t,t^2\rangle$$

• $\myv r(t)=\langle t,t^2 \rangle$
• $x(t)=t;\ \ \ y(t)=t^2$
• In this case we can write $y$ as a function of $x=t$: $$\nonumber y=x^2$$ and we know what that looks like...
• Mathematica: use ParametricPlot (2-d) and ParametricPlot3d:
  ParametricPlot[{t, t^2}, {t, 0, 3}]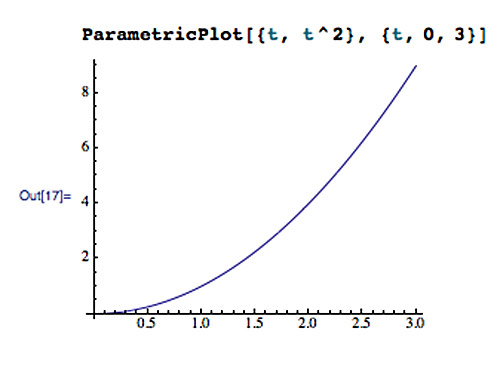
  

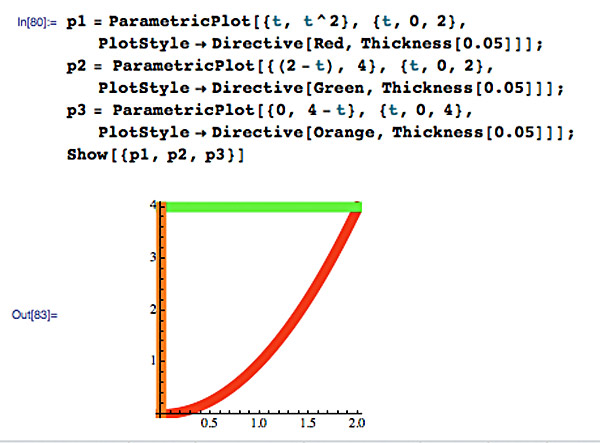
Plotting curves

...from discrete segments. For example:

In Mathematica:

Your turn

...to write parametric expressions to produce these paths:

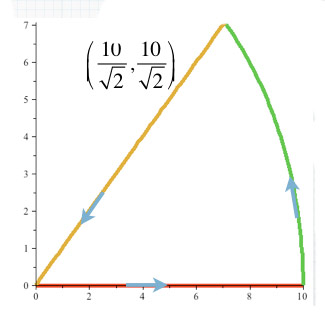
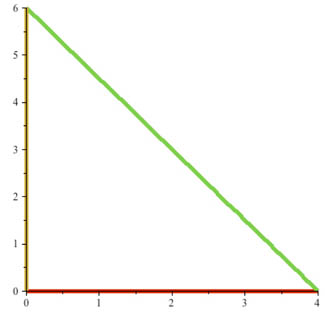
For the segment-of-a-circle: Think of the polar coordinate representation of a circle, in which the radius, $r$, is constant, as the angle, $\theta$, varies. Now, use the transformations of $r,\theta \to x(r,\theta), y(r,\theta)$ to find an expression in Cartesian coordinates for a circle in terms of the constant radius, and the changing (*parameter*) $\theta$.

3-d example

$$\myv r(t)=\langle 1+t, 2+5t, -1+6t \rangle\nonumber$$

• $x(t)=1+t$
• $y(t)=2+5t$
• $z(t)=-1+6t$

ParametricPlot3D[{1+t,2+5*t,-1+6*t},{t,0,10}]

Using 3-d surfaces

...to graph and visualize vector equations.

Consider: $$\myv r(t)=\langle \cos t, \sin t, t\rangle\nonumber$$

• $\cos^2 t + \sin^2 t = x^2+y^2=1$.
• In 2-d this is the equation of points on a circle of radius 1.
• So in 3-d, the path traced out by $\myv r(t)$ must lie on the surface of the cylinder $x^2+y^2=1$
  

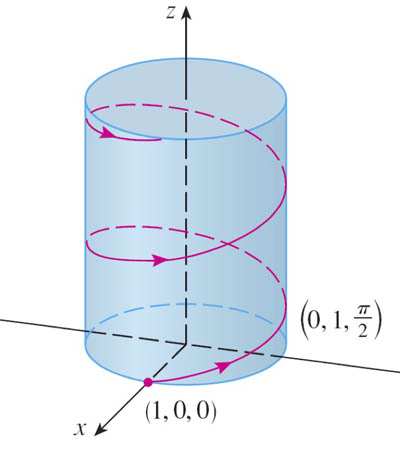
This process of ignoring one coordinate, and seeing how 2 of the coordinates relate to each other without regard to the other one is like "projection". Doing this with the other coordinate pairs, we see the familiar-looking relations: $$\nonumber x=\cos z;\ \ \ y=\sin z$$

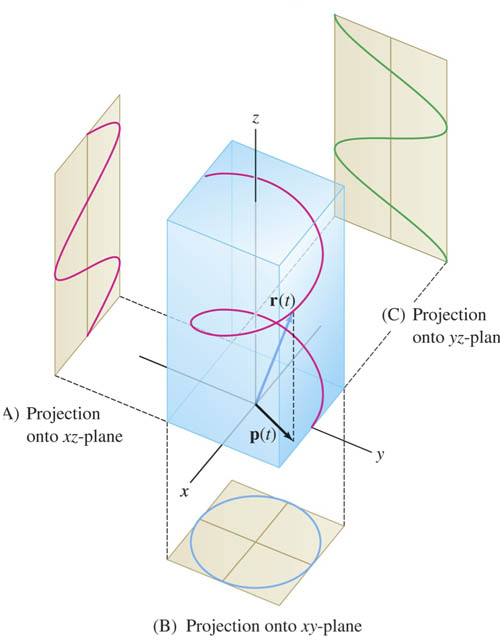
Intersections and projections

Consider $$\myv r(t)=\langle t,t^2,t^3 \rangle \nonumber$$

Since $y(t)=t^2$ and $x(t)=t$ we can combine these equations to get $$\nonumber y=x^2.$$

And similarly $$\nonumber z=x^3,$$ so we could plot the 3-d surfaces

• $y=x^2$ (for any $z$), and
• $z=x^3$ (for any $y$)

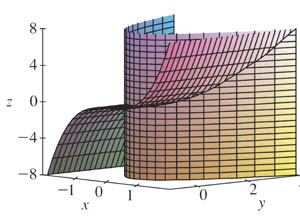The points in $\myv r$ need to be on *both* of those surfaces, so we could look for $\myv r$ as the intersection of the surfaces.

Traces of $\langle t,t^2,t^3 \rangle$

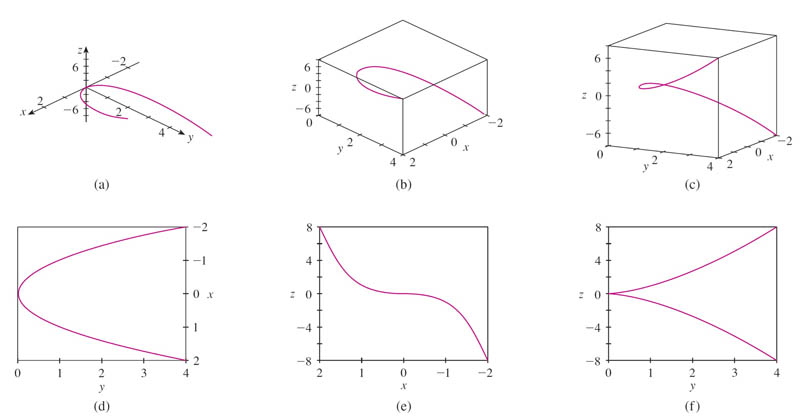
To Do

• Handout: Projections