Arc length and curvature [10.3]

The Nowitna river (Alaska) - How long is it?
- Calculating arclength and curvature
- Arclength is independent of the choice of parameter used to describe a curve.
- Re-parameterizing a curve - using the arclength as the parameter.
- Geometric definition of curvature.
- The TNB frame (Tangent - Normal - Binormal unit vectors).
Arclength
$\myv r(t)$ is a vector function.
$$\myv r(t)=\langle f(t),g(t),h(t)\rangle\nonumber;
\ \ t_i\leq t\leq t_f.$$
where $\myv r(t_i)=\myv a$ and $\myv r(t_f)=\myv b$
The tip of the position vector $\myv r(t)$ traces a curve (trajectory) in space which
looks schematically like:

- The arclength is the distance along the curve from $\myv a$ to $\myv b$.
- Arclength is a scalar.
- It is not the distance "as the crow flows" of a vector starting at $\myv a$ and terminating at $\myv b$.
The arclength from is approximately equal to the sum of the The derivative $\myv r'(t)$ is a vector tangent to the curve. Its magnitude is the "speed" of a particle moving in time, $t$, according to $\myv r(t)$. So, the arclength is approximately
$$L\approx \sum |\myv r'(t)|\Delta t\nonumber.$$
In the limit of ever smaller $\Delta t\to dt$, the sum approaches the integral...
$$\begineq L&=&\int_a^b |\myv r'(t)|\,dt\\
&=&\int_a^b \sqrt{\left(\frac{df}{dt}\right)^2
+ \left(\frac{dg}{dt}\right)^2
+ \left(\frac{dh}{dt}\right)^2
}\,dt
\\
&=&\int_a^b \sqrt{\left(f'(t)\right)^2
+ \left(g'(t)\right)^2
+ \left(h'(t)\right)^2
}\,dt
\endeq
$$
It looks like
$$ 0 \leq t \leq 2\pi,$$
the derivative is
$$ \myv r'(t) = \langle -\sin t, \cos t,1\rangle,\nonumber$$
and so...
$$|\myv r'(t)| = \sqrt{(-\sin t)^2 + (\cos t)^2 +1}=\sqrt 2.\nonumber$$
Substituting into the arclength expression
$$L =\int_0^{2\pi} \sqrt 2 \,dt=2 \sqrt 2 \pi.\nonumber$$
$$s(t) = \int_a^t |\myv r'(u)| du
=\int_0^t\sqrt{\left(\frac{dx}{dt}\right)^2 +
\left(\frac{dy}{dt}\right)^2+
\left(\frac{dz}{dt}\right)^2
}
\,dt$$.
This means that
$$\frac{ds}{dt}=|\myv r'(t)|.$$
[Sorry, I can't bear to write "parametrization" as Stewart does.]
It may be useful (and is certainly beautiful) to re-parameterize a curve in terms of
The arclength along a curve
We could use the arclength ("distance along the curve") as the parameter to describe a curve (instead of the time, or angle, or some other parameter).
Example -- $\myv r(t)=\langle \cos t,\sin t,t\rangle$:
Reparametrize with respect to arc length, beginning at (1,0,0) in direction of increasing $t$.
This depends on being able (easily or otherwise) to take $s(t)$ and invert it to $t(s)$.
This is a technique used in General Relativity: We talk about the "proper time" measured along the the space-time trajectory of a particle as a quantity that all observers agree on.
The question: How to describe "curvature" in a useful way?
The curvature should be...
Can you think of a situation in which the acceleration is not zero, even though the curvature of the path is zero?
Acceleration in a straight line.
The unit tangent
$$\uv T(t)=\frac{\myv r'}{|\myv r'|}$$ is a vector quantity that is always the same length, no matter what the velocity $\myv r'$ is. So, what about
$$\frac{d\uv T(t)}{dt}?$$
What's the problem with that?
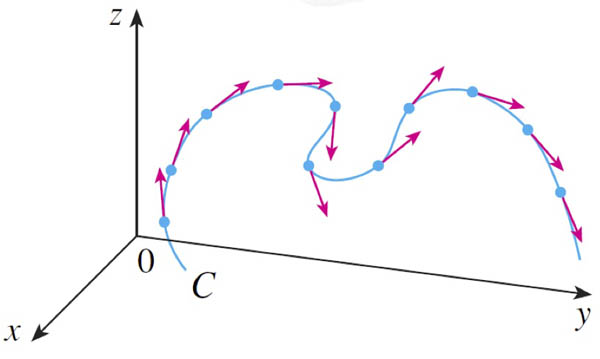
In this picture, the unit tangent vectors are evenly spaced along the curve: ...We should look at how $\uv T$ changes with respect to changes in the arclength, $s$, (instead of w.r.t time $t$):
The curvature, $\kappa$, is
$$\kappa = \frac{d\uv T}{ds},$$
the rate of change of unit tanget vector direction with respect to arclength.
By the chain rule, this is
$$\kappa = \left|\frac{d\uv T}{dt}\right| \frac{dt}{ds} = \frac{|d\uv T(t)/dt|}{|\myv r'(t)|} .$$
It seems like a circle ought to have a constant curvature. Let's see...
Circle of radius $a$:
$$\myv r(t)=a \cos t\uv i + a \sin t\uv j.$$
$$\myv r'(t)=-a\sin t \uv i + a \cos t\uv j.$$
$$|\myv r'(t)| = \sqrt{(-a\sin t)^2+(a\cos t)^2}=a.$$
$$\uv T(t) = \myv r'(t)/|\myv r'(t)|=\myv r'(t)/a=- \sin t \uv i+\cos t\uv j.$$
$$\uv T'(t) =- \cos t \uv i - \sin t\uv j.$$
$$|\uv T'| = \sqrt{(-\cos t)^+(-\sin t)^2}=\sqrt{\cos^2 t+\sin^2 t} = 1.$$
$$\kappa = \frac{|\uv T'(t)|}{|\myv r'(t)|}=\frac{1}{a}.$$
This suggests a geometric definition of curvature...
We had:
$$\kappa = \left|\frac{d\uv T}{dt}\right| \frac{dt}{ds} = \frac{|d\uv T(t)/dt|}{|\myv r'(t)|} =
\frac{\left|\frac{d}{dt}\left[ \frac{\myv r'(t)}{|\myv r'(t)|}\right]\right|}{|\myv r'(t)|}.$$
Theorem: The curvature of the curve given by $\myv r(t)$ is given by:
$$ \kappa(t)=\frac{|\myv r'(t)\times \myv r''(t)|}{|\myv r'(t)|^3}.$$
...uses the formula above to calculate the curvature of the 'twisted cubic' $\myv r(t)=\langle t,t^2,t^3 \rangle$:
$$\kappa(t)=\frac{2\sqrt{1+9t^2+9t^4}}{(1+4t^2+9t^4)^{3/2}}$$
The twisted cubic...[plot the twisted cubic.]
[Graph $\kappa(t)$ to see...]
Several quantities, defined in terms of derivatives of $\myv r(t)$:
The unit tangent vector is
$$\uv T(t) \equiv \frac {\myv r'(t)}{|\myv r'(t)|}.$$
Under what circumstances is $\uv T'(t)=0$?
(That is to say, $\uv T'\equiv \frac{d}{dt}\uv T$ is not necessarily a unit vector.)
But when $|\uv T'(t)|\neq 0$...
The unit normal vector is
$$\uv N(t) \equiv \frac {\uv T'(t)}{|\uv T'(t)|}.$$
$\uv N$ points towards the center of the osculating circle for $\myv r(t)$.
What's the magnitude of the cross product of two unit vectors, which are at right angles?
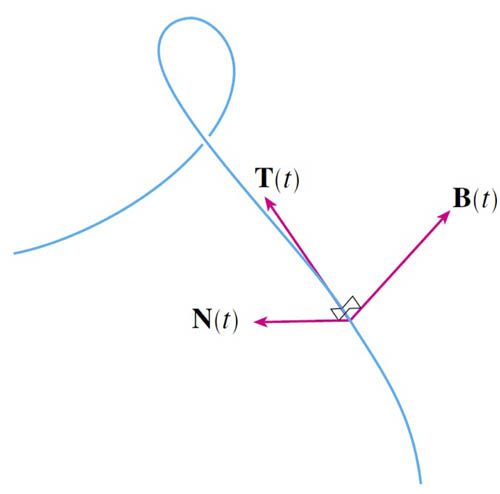
The binormal vector is
$$\myv B(t)=\uv T(t)\times\uv N(t).$$
We may as well write it as $\uv B(t)$ because it must have unit length by this definition.
For $\myv r(t)=2\cos t \uv i + 2\sin t \uv j + 3t \uv k$: Find $\uv T$, $\uv N$, and $\uv B$ at $t=3\pi/2$. Sketch these on a plot of $\myv r(t)$. See 10.3.TBN.nb for calculations
Since distance = speed (times) time, we can approximate the distance $\Delta L$ moved in a time interval $\Delta t$ as
$$ \Delta L \approx \left| \myv r'\right| \Delta t\nonumber$$
Example
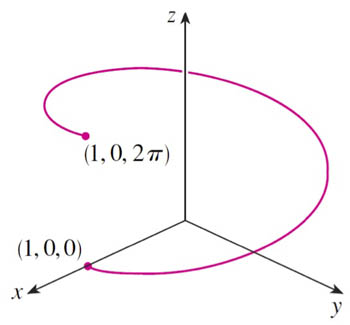 Find the length of the arc of the helix that obeys the equation
$$\nonumber \myv r(t)=\langle \cos t, \sin t, t \rangle$$
from the point $(1,0,0)$ to $(1,0,2\pi)$.
Find the length of the arc of the helix that obeys the equation
$$\nonumber \myv r(t)=\langle \cos t, \sin t, t \rangle$$
from the point $(1,0,0)$ to $(1,0,2\pi)$.
Arclength distance function
 The arclength distance function $s(t)$, where $s(0)=0$,
The arclength distance function $s(t)$, where $s(0)=0$,
Parameterizations
Re-parameterization
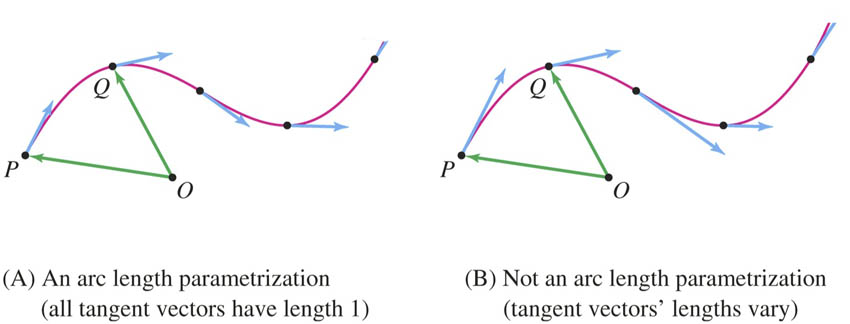
Curvature
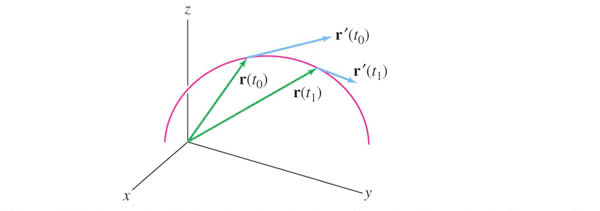 The velocity vector $\myv r'(t)$ is tangent to the curve at each position on the curve. So, as the direction of a curve changes,the velocity vector will also change. So our first attempt to quantify the idea of "curvature" might be to look at at the change of the velocity vector, that is, the acceleration:
$$\myv a (t)= \frac{d\myv r'(t)}{dt}$$
The velocity vector $\myv r'(t)$ is tangent to the curve at each position on the curve. So, as the direction of a curve changes,the velocity vector will also change. So our first attempt to quantify the idea of "curvature" might be to look at at the change of the velocity vector, that is, the acceleration:
$$\myv a (t)= \frac{d\myv r'(t)}{dt}$$
 Does this suggest a useful way to think about curvature?
Does this suggest a useful way to think about curvature?
Curvature of a circle
Osculating circle

The circle with the same curvature (that is, radius=$1/\kappa$) as $\myv r(t)$ at a point $P$ on the curve.
Another way to calculate curvature
Example 4 - group work
Unit tangent, unit normal, binormal
Example

Image credits