Motion in space [10.4]
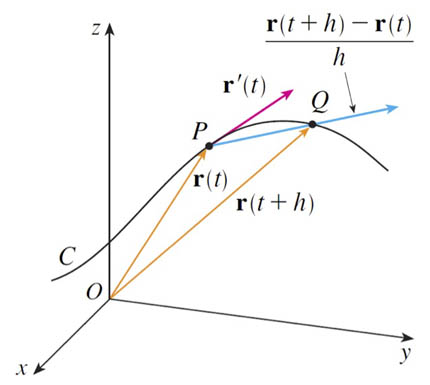 If $\myv r(t)$ represents the vector position of a point particle in space, as a function of time $t$, then the velocity vector is...
If $\myv r(t)$ represents the vector position of a point particle in space, as a function of time $t$, then the velocity vector is...
$$\myv v(t)\equiv\lim_{h\to 0}\frac{\myv r(t+h)-\myv r(t)}{h}=\myv r'(t) \equiv \dot{\myv r}(t).$$
Speed
$$|\myv v(t)|\equiv |\myv r'(t)| = \frac{ds}{dt}\equiv v(t).$$
So the scalar speed $v(t)$ only conveys the magnitude of the velocity vector, nothing about its direction.
Acceleration
$$\myv a(t)\equiv \myv v'(t)=\myv r''(t)\equiv \ddot{\myv r}(t).$$
And we can also write acceleration as the limit of the change in velocity per unit time $$\myv a(t)=\lim_{\Delta t\to 0}\frac{\myv v(t+\Delta t) - \myv v(t)}{\Delta t}.$$
Integrating...
$$\myv v(t)=\myv v(t_0)+\int_{t_0}^t \myv a(u)\,du.$$
$$\myv r(t)=\myv r(t_0)+\int_{t_0}^t \myv v(u)\,du.$$
Projectile motion
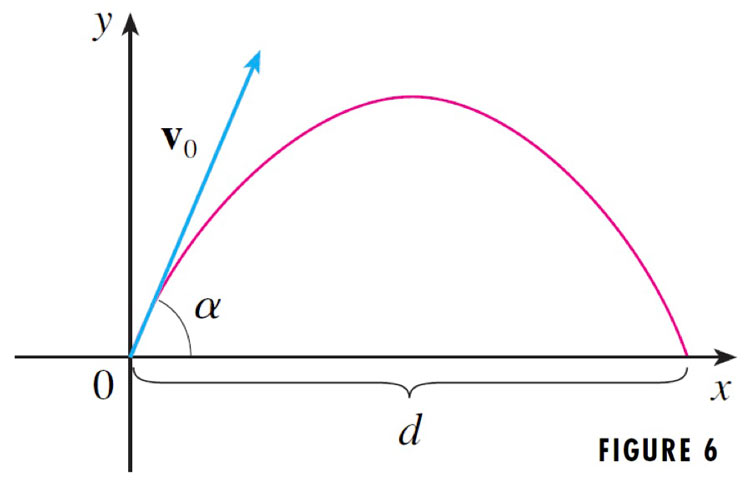
Acceleration due to gravity is constant, and always *down*.
Newton's law, $\myv F=m\myv a$: The only force acting on the projectile is gravity. The gravitational force is the object's weight, $mg$ (where $g=9.8$ m/s${}^2$). $$\myv F=-mg \uv j = m(a_x(t) \uv i+a_y(t) \uv j.$$
In the vertical direction ($\uv j$ component) this becomes: $$-g=a_y(t)=v_y'(t)$$ Integrating as above and saying that $t=0$ is the time of launch (so that $v_y(0)=v_0\sin\alpha$ and $v_x(0)=v_0\cos\alpha$) we get: $$v_y(t)=v_0\sin\alpha-gt.$$ Integrating once more, as above, gives: $$y(t)=(v_0\sin\alpha) t-\frac12gt^2.$$
Going through a similar process, the horizontal position is found to be: $$x(t)=(v_0\cos\alpha) t.$$
See the Catapult worksheet
Acceleration- components
Interesting things happen when we resolve acceleration into components parallel (tangential) and perpendicular (normal) to the velocity...
Since the unit tangent vector $\uv T=\frac{\myv r'(t)}{|\myv r'(t)|}=\frac{\myv v}{v}$, $$\myv v= v\uv T.$$
Differentiating both sides of this equation, using the product rule on the right, gives us $$\myv v' = \myv a = v' \uv T + v \uv T'.\label{accel}$$
Now re-writing 2 relations from 10.3 in terms of velocity/speed: The curvature, $\kappa$, $$\nonumber \kappa = \frac{|\uv T'|}{|\myv r'|}= \frac{|\uv T'|}{v},$$ and the unit normal vector $\uv N=\uv T'/|\uv T'|$, $$\nonumber \uv T' = |\uv T'| \uv N=\kappa v \uv N.$$
Substituting into \ref{accel},
$$\myv a = v' \uv T +\kappa v^2 \uv N.$$
- No $\uv B$ component (binormal) to the acceleration??!!
- This means that acceleration is always in the $\uv T$-, $\uv N$-plane.
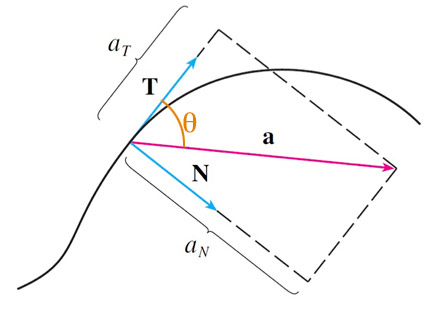 A change in speed, $v'$ only affects the tangential component, $a_T$.
A change in speed, $v'$ only affects the tangential component, $a_T$.
- The normal component of acceleration, $a_N$, is only sensitive to speed^2 and curvature, not the change in speed.
- Newton's law is: $\myv F = m \myv a$.
- So, the "sideways force" that the rails/road exerts on a train/car in order to keep it on the track/road is the normal component of the force (also called the centripetal force):
$$F_N=ma_N=m\kappa v^2.$$
There is a maximum sideways force that rails can exert before a train "hops the rails"...
"Twice the speed limit"...
If you double the speed, the sideways force needed to stay on the rails quadruples.
Components in terms of $\myv a$
$$\myv a(t)=a_T(t) \uv T(t)+a_N(t)\uv N(t).$$

[In what follows, I'll stop writing the explicit time dependence, but just remember that all the quantities we're dealing with are time dependent.]
The tangential component, $a_T$ is the dot product of $\myv a$ with a unit vector in the tangential direction, namely $\uv T$: $$\begineq a_T&=&\myv a\cdot\uv T\\ &=&\myv a \cdot \frac{\myv v}{|\myv v|}=\frac{\myv a\cdot \myv v}{v}.\\ \endeq$$
We can write the dot product as $\myv a \cdot \uv T=a \cos \theta$, where $\theta$ is the angle between $\myv a$ and $\uv T$.
Since $\uv T \perp \uv N$, We could write $$\nonumber a_N=\myv a \cdot \uv N = a \sin \theta.$$
But $|\myv a \times \uv T| = a \sin \theta$ too, so
$$\begineq a_N &=& |\myv a \times \uv T| \\ &=& \left|\myv a \times \frac{\myv v}{v} \right| = \frac{|\myv a \times \myv v|}{v} .\endeq$$

Summary
Unit tangent vector
$$\uv T = \frac{\myv v}{v}$$
Unit Normal vector
$$\uv N = \frac{\uv T'}{|\uv T'|}$$
Decomposition of acceleration
$$\uv a(t)=a_T(t) \uv T(t) + a_N \uv N(t)$$
Tangential component
$$a_T=v'=\frac{\myv a \cdot \myv v}{v}$$
Normal component
$$a_N=\kappa v^2 =\frac{|\myv a \times \myv v |}{v}$$
$$a_N \uv N=\myv a -a_T\uv T = \myv a - \frac{\myv a \cdot \myv v}{\myv v\cdot\myv v}\myv v$$
For example
With this vector function for position: $$\myv r(t)=t^2\uv i + t^2\uv j+t^3\uv k,$$
the velocity is $$\myv v(t)=\myv r'(t)=2t\uv i + 2t\uv j+3t^2\uv k.$$
The speed is $$|\myv v|=\sqrt{4t^2+4t^2+9t^4}=\sqrt{8t^2+9t^4}.$$
the acceleration is $$\myv a(t)=\myv r''(t)=2\uv i + 2\uv j+6t\uv k.$$
Tangential component of acceleration $$a_T=\frac{\myv a \cdot \myv v}{v}=\frac{8t+18t^3}{\sqrt{8t^2+9t^4}}.$$
Normal component of acceleration $$ a_N=\frac{|\myv a \times \myv v |}{v}=\frac{6\sqrt 2 t^2}{\sqrt{8t^2+9t^4}}, $$ using... $$\begineq \myv a \times \myv v&=&\left|\begincv \uv i&\uv j&\uv k \\ 2&2&6t\\ 2t&2t&3t^2 \endcv\right| \\ &=&(6t^2-12t^2)\uv i + (12t^2-6t^2)\uv j + (4t-4t)\uv k\\ &=&-6t^2\uv i +6t^2 \uv j \endeq $$