Parametric surfaces [10.5]

Walt Disney concert hall, Los Angeles, architect: Frank Gehry
- Alternate ways to describe a surface,
- In high symmetry situations, a different parameterization may be simpler (than Cartesian coordinates!)
- Eventually we'd like to answer questions like "how much aluminum will we need for that concert hall roof?".
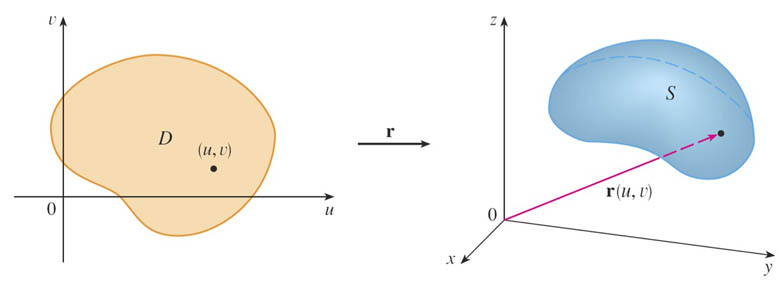
A vector function $\myv r(t)=\myc{f(t),g(t),h(t)}$ of a single parameter described a curve in space.
- Suppose that $$\nonumber \myv r(u,v)=\langle x(u,v), y(u,v), z(u,v) \rangle$$ is a vector-valued function,
- Defined on a region $D$ of the $u$- $v$-plane.
- As $(u,v)$ varies throughout $D$, then $\myv r$ traces out a surface $S$ in 3 dimensions.
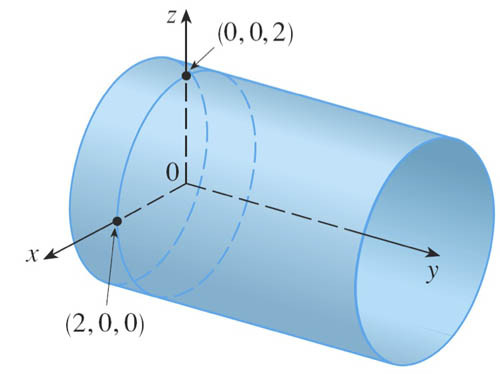
Example: cylinder
$$\myv r(u,v)=\langle 2\cos u, v, 2\sin u \rangle$$
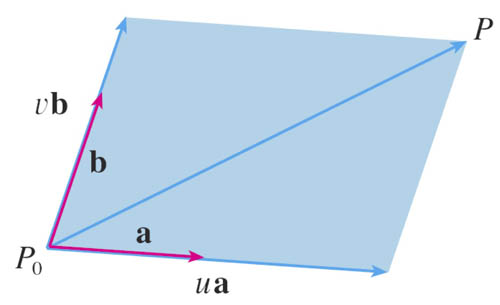
Example: plane
$$\myv r(u,v)=\myv r_0 + u\myv a+v\myv b$$
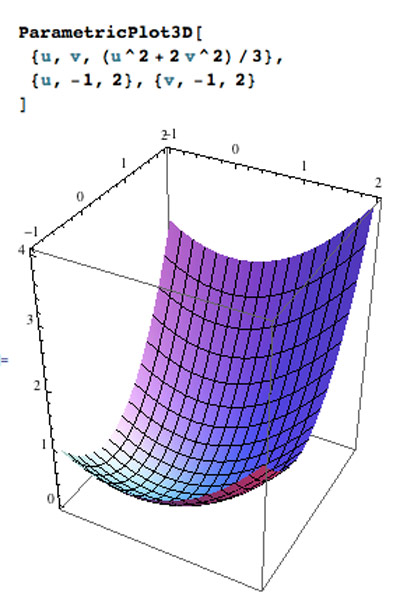
$x$ and $y$ as 'parameters'
Plot the surface defined by $$z=\frac{x^2+2y^2}3.$$
For our two parameters, we could just use $u=x$, $v=y$, and then $z=\frac{u^2+2v^2}3.$
Turning this into a vector function of $u$ and $v$: $$\myv r=\langle u, v, (u^2+2v^2)/3 \rangle$$
Choosing parameters based on symmetries/forms
See 10.5.nb.
Consider the points that fulfill: $$\frac{x^2}{4}+y^2+\frac{z^2}{4} = 1$$
You could solve for $z$: $$z=\pm\sqrt{4\left( 1-\frac{x^2}{4}-y^2 \right)} $$ and plot $\myc{x, y, z(x,y)}$.
Or, we re-arrange the equation into $$x^2+z^2 = 4(1-y^2).$$ We recognize the left side as the equation for a circle with a radius $\sqrt{4(1-y^2)}$ that depends on $y$.
This suggests that we write the *radius* as one of the parameters, $u=2\sqrt{1-y^2}$ (and inverting: $y=\sqrt{1-\frac14 u^2}$), and then we could write $x$ and $y$ in terms of a "polar angle" parameter $v$ sweeping around a circle of radius $u$ like this: $$\myv r(u,v)=\myc{u\cos v,\sqrt{1-\frac14u^2},u\sin v}$$
Todo
- Bagels, bagels, bagels