Functions of several variables [11.1]
Tabular data
Things that depend on more than one variable.
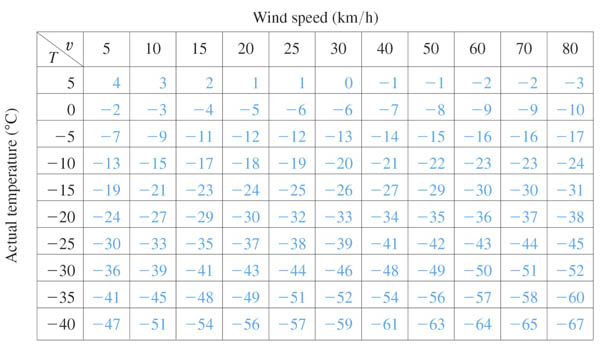
$T_w(T,v)$: A table of wind chill temperature, $T_w$
(in $^o$C) which depends on the air temperature, $T$, and the speed of the wind, $v$.
Domain and range
Consider the function $$g(x,y)=\sqrt{9-(x^2+y^2)}.$$
In order that the function evaluate to something non-imaginary, the greatest possible domain is $\{x,y: x^2+y^2\leq 9\}$.
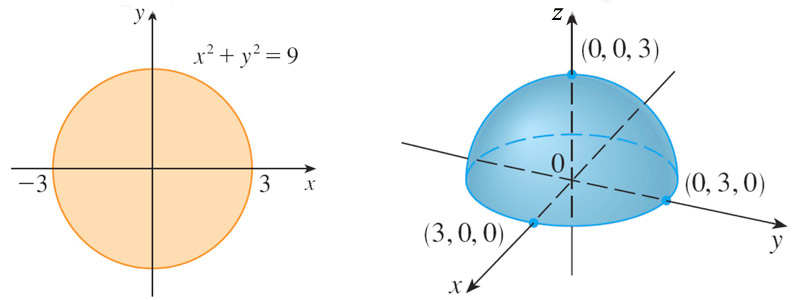
The function can be plotted as a surface, with $z=g(x,y)$, and we see that the corresponding range is $0 \leq z \leq 3$.
Level curves / contours
One way of visualizing the 3-d surface in 2-d is to plot level curves: Cross-sections of the surface at a discrete set of height values $\{ k\}$.
You consider a particular $z$-height, setting $k=g(x,y)$, and then sketch the resulting curve in the $x$-, $y$-plane.
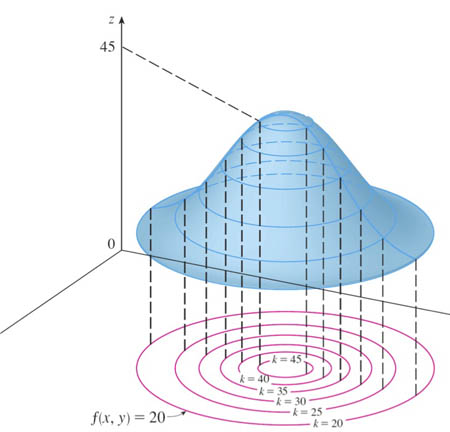For a function of 2 variables, $g(x,y)$ we plot level curves $k=g$.
To do
- Drawing contours
Visualizations
A couple different ways to visualize surfaces in 3-d...
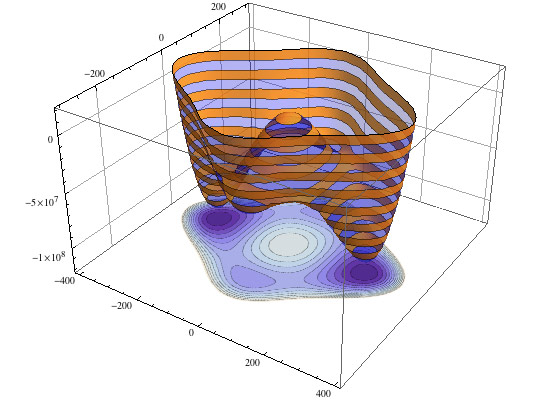
Consider two functions: $$f(x,y)=12-x-y;\ \ \ g(x,y)=\frac{-9y}{x^2+y^2+1}.$$
Surface plots
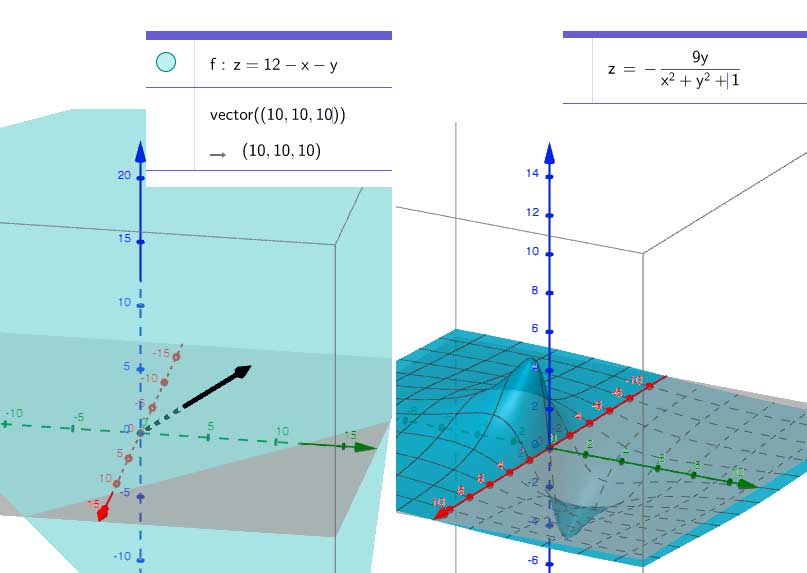
Contour plots
- Sagemath and Mathematica color the lower heights darker by default.
- How can you tell from the contour plot, where the height is changing most rapidly? When the surface is flat?
- How can you tell from the contour plot how to move away from point A in such a way that the height will not change?
- How can you estimate the value of the function at point B?
Todo
- Using contour plots
Surface plot with contours
You can display contours on the surface plot (rather than a rectangular mesh) with this command:
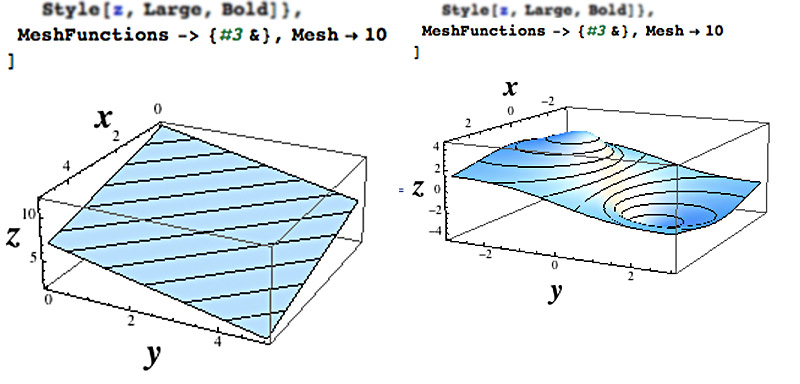
- #3 refers to the 3-rd coordinate, $z$
- Mesh -> 10 tells Mathematica to display 10 constant-$z$ lines, equally spaced in $z$.
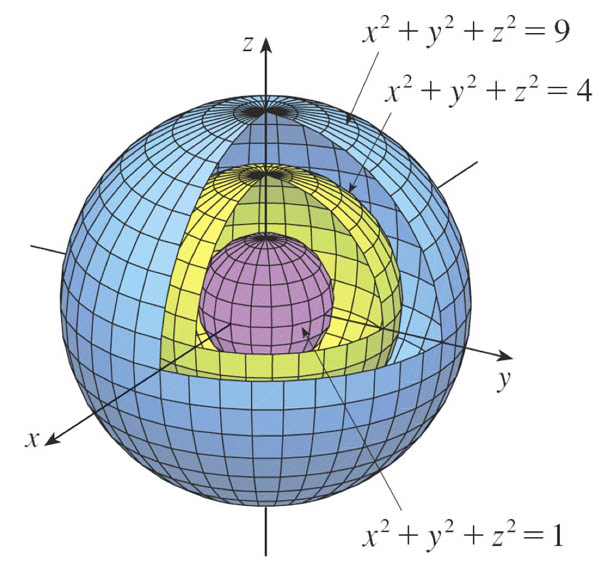
Level surfaces of 3 variables
For a function, $h(x,y,z)$ of 3 variables, the mathematical entities $k=h$ are level surfaces.
More glitz...
It's possible to combine surface plots and corresponding contour plots all in the same figure (click it to see the underlying notebook)...
