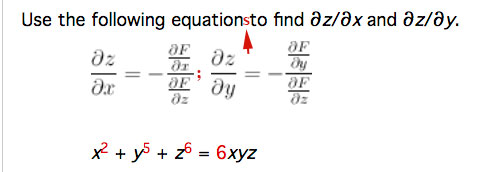The Chain Rule

...a chain of events.
When we take about the chain rule, we're referring to an image of a chain of events.
1-d chain rule
If $y=f(x)$, and in turn $x=g(t)$ then the chain rule in an easy-to-remember form is: $$\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}.$$
Examples
$$y(x)=x^3;\ \ x(t)=\ln t;\ \ \Rightarrow y(x(t))=(\ln t)^3.$$
$$\frac{dy}{dx}=3x^2; \frac{dx}{dt}=\frac1t$$
$$\Rightarrow \frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}=3x^2 \frac1t=\frac{3(\ln t)^2}{t}.$$
Another way of talking about the chain rule is to call $y(x)$ the "outside" function, and $x(t)$ the "inside" function. Then, we say that we take the derivative of the outside function (wrt to the inside function), and then multiply by the derivative of the inside function. I think about "putting off" evaluating $x'(t)$ until the very end...x
To differentiate $y(t)=\frac{1}{7t}$ the outside function is $y(x)=\frac{1}{x}$, and the inside function is $x(t)=7t$. $$\begineq\frac{d}{dt}\(\frac{1}{x}\)&=&\frac{d}{dt}(x)^{-1}= =\frac{d}{dx}\left(x^{-1}\right)\frac{d}{dt}(x)\\ &=&-1(x)^{-2}\frac{d}{dt}(x) =\frac{-1}{(7t)^2}(7)\\ &=&-\frac{1}{7t^2} \endeq $$
Multivariable chain rule
Our hiking approximation: $$ \Delta z \approx f_x \Delta x + f_y \Delta y$$
If $z=f(x,y)$ and in turn $x=g(t)$ and $y=h(t)$ are parametric functions of $t$, then $z$ must ultimately be a function of $t$ as well: $z=z(t)$.
The $\Delta$ symbols mean: $\Delta z= z(t+\Delta t)-z(t)$, $\Delta x= x(t+\Delta t)-x(t)$, and $\Delta y= y(t+\Delta t)-y(t)$.
Now divide both sides of the hiking approximation by $\Delta t$: $$ \frac{\Delta z}{\Delta t} \approx f_x \frac{\Delta x}{\Delta t} + f_y \frac{\Delta y}{\Delta t}$$
In the limit $\Delta t\to 0$ these change ratios become differentials approximate relation becomes exact...(and substituting in the definitions of $f_x$ and $f_y$ in terms of $z$)
$$ \frac{dz}{dt} = \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}.$$ This is "Case 1" of the multi-variable chain rule.
This also shows the difference between partial derivatives and exact derivatives).
For example, if $f(x(t),y(t))=\sin(xy^2)$, $$\begineq \frac{dz}{dt}&=& \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}\\ &=& \cos(xy^2)\cdot y^2 \frac{dx}{dt} + \cos(xy^2)\cdot x2y \frac{dy}{dt}\\ &=& y\cos(xy^2)\left[y \frac{dx}{dt} + 2x \frac{dy}{dt}\right]. \endeq$$
I use the derivatives (e.g. $d/dt$) when writing about a function that depends on just one variable. I use the partial derivatives (e.g. $\del/\del x$) when talking about a rate of change of a function that depends on more than one variable (and implicitly, the other variables are held constant while calculating the partial derivative).
[Now go to topic 11.6 before returning for more on the chain rule.]
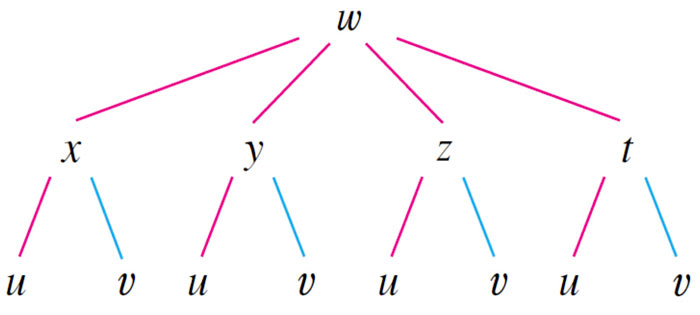
Chain rule for more than one independent variable
Example
4 intermediate variables which each depend on 2 total independent variables
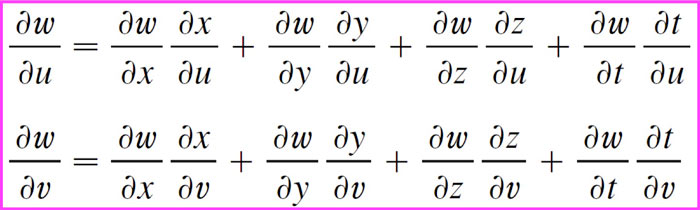
Implicit differentiation
[WebAssign #6] The textbook starts by differentiating a function $F(x,y,z)=0$. The development results in *2* equations: