Lagrange multipliers
How to find peaks, or valleys, along a particular path?
1st approach
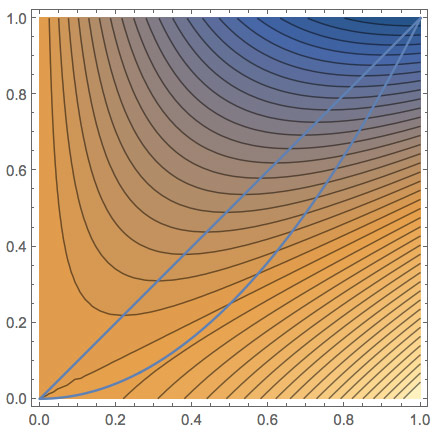
In the kitten problem, $T(x,y)=x^2-2xy$, you guessed that the highest temperature occurred on the bottom blue boundary, as close to the next-highest contour line outside as possible.
Now try another approach:
- Parameterize the blue path, $y=x^2$, coming up with $x(t)$ and $y(t)$,
- Find $z(t)=T(x,y)=T(x(t),y(t))$
- Find critical points: $t$ such that $dz/dt=0$. If more than one, figure out the maxima.
- Use that $t$ to find coordinates $x(t)$ and $y(t)$.
What are the coordinates of the point along the boundary with the highest temperature?
Now we'll consider another way...
The gradient and contour lines
$z=f(x,y)$ is the equation for a surface in three dimensions.
What we mean by a "contour line":
- $f(x,y)=k$ is a level curve or contour line.
- A contour line is a curve graphed in the $xy$ plane. (Not in 3-dimensions.)
The gradient at a point $(x_0,y_0)$ in the $xy$ plane:
- $$\begineq \myv \grad f(x_0,y_0)&=&f_x(x_0,y_0)\uv i +f_y(x_0,y_0)\uv j\\ &\equiv&\left.\frac{\del f(x,y)}{\del x}\right|^{(x_0,y_0)} \uv i +\left.\frac{\del f(x,y)}{\del y}\right|^{(x_0,y_0)} \uv j \endeq$$
- It points in the direction of maximum slope of the surface $z=f(x,y)$.
- But the gradient is a vector in the $xy$ plane. (Not in 3-dimensions).
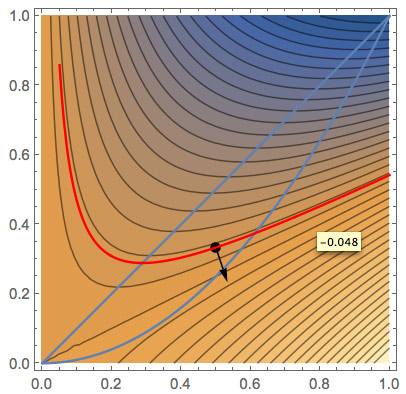
- The gradient at $(x_0,y_0)$ is always perpendicular to the contour line $f(x,y)=k=f(x_0,y_0)$.
At every point along the 2-d curve $f(x,y)=k$, the gradient $\myv \grad f$ is a normal vector of the curve.
Using gradients to find extreme points
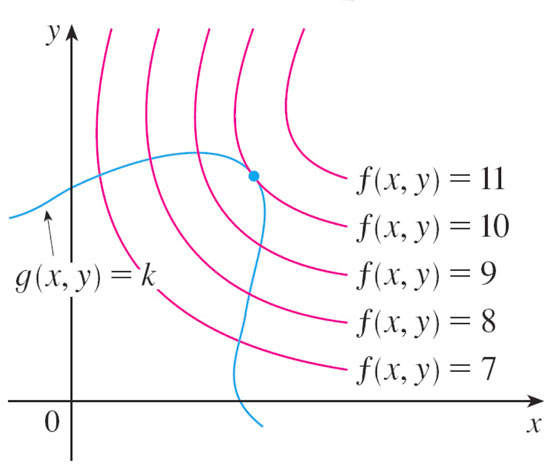
Imagine that you are hiking along a path specified by the equation $g(x,y)=k$ through a landscape where the height is specified by $f(x,y)$. How do you find the highest point of your hike?
In mathematical terms:
- Try to find the extreme values of $f(x,y)$...
- Subject to the constraint $g(x,y)=k$.
We seek the the extreme values of $f(x,y)$ when the point $(x,y)$ is restricted to lie on the level curve $g(x,y)=k$.
E.g. maximizing $f(x,y)$ means finding the contour $f(x,y)=c$ that $g(x,y)$ touches, where $c$ has the largest possible value.
It looks like this happens when the desired contour of $f$ is tangent to $g(x,y)=k$.
[If $g$ is not tangent to a particular contour of $f$, then there exists a point on $g$ which is higher, and one which is lower on either side of their intersection.]
Tangent means that the normal vectors to the 2-d curves $g=k$ and $f=c$ are parallel (one is the scalar multiple of the other).
We know $\myv \grad f$ is always normal to any 2-d contour line of $f$. Ditto for $\myv \grad g$ along the particular contour line $g=k$. Therefore...
At the location $(x_0,y_0)$ where the two contours are tangent: $$\myv \grad f(x_0,y_0) = \lambda \myv \grad g(x_0,y_0)$$ where $\lambda$ is some scalar.
The method of Lagrange multipliers
Kitten, re-re-visited
$$T(x,y)=x^2-2xy$$ The gradient of this function.. $$\myv\grad T =T_x\uv i + T_y\uv j= (2x-2y)\uv i -2x\uv j.$$
We're interested in the the highest contour of $T$ along the path $y=x^2$.
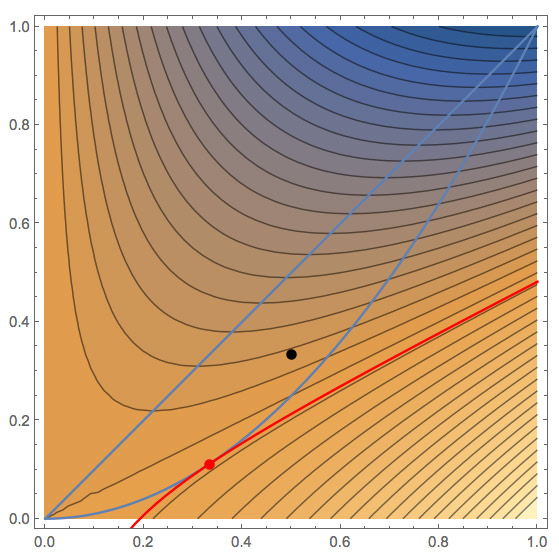
We need to express the path $y=x^2$ in the form of $g(x,y)=k$... How about
$$g(x,y)=x^2-y=0?$$
We can calculate the gradient of this function... $$\myv\grad g=2x \uv i -1\uv j.$$
The condition that the gradients are parallel, $\myv \grad T = \lambda \myv \grad g$, leads to one equation for the $x$-components: $$2x-2y=\lambda 2x$$ and one for the $y$-components: $$-2x = -\lambda.$$
Using the two to eliminate the scalar $\lambda$: $$2x-2y=(2x)2x=4x^2$$ Taking into account our constraint equation, that $y=x^2$, leads to one equation for $x$: $$\begineq 2x-2(x^2)&=&4x^2\\ 1-x&=&2x \endeq$$ The solution is $x=1/3$, $\Rightarrow y=1/9$. Hopefully the same location we found by parametric means?!
Solve ing simultaneous equations in Cocalc
[or in Mathematica
Two constraints?
Suppose that we want to find...
- the maximum or minimum values of a function $f(x,y,z)$,
- subject to two constraints: $h(x,y,z)=c$ and $g(x,y,z)=k$.
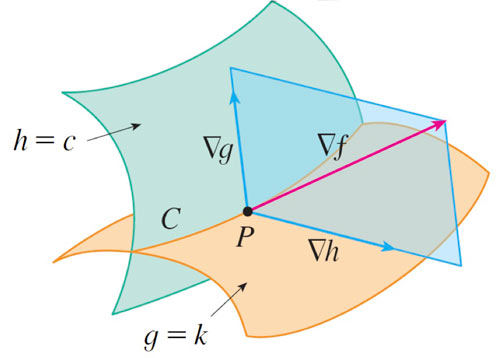Geometrically, we are looking for the extreme values of $f$ when $(x,y,z)$ lies on the curve of intersection, $C$, of the level surfaces
$h(x,y,z)=c$ and $g(x,y,z)=k$. Which can be expressed as...
$$\myv\grad f(x_0,y_0,z_0) = \lambda\myv\grad g(x_0,y_0,z_0) + \mu\myv\grad h(x_0,y_0,z_0)$$
where $\lambda$ and $\mu$ are scalars.
This amounts to solving these five equations... $$f_x=\lambda g_x +\mu h_x$$ $$f_y=\lambda g_y +\mu h_y$$ $$f_z=\lambda g_z +\mu h_z$$ $$g(x,y,z)=k$$ $$h(x,y,z)=c$$ for the five unknown quantities $\lambda$, $\mu$, $x$, $y$, and $z$.
ToDo
- Lagrange Multiplier Problems: *Do* use CoCalc to solve the systems of equations.
- ANSWERS (*.pdf file) to the Lagrange Multipliers Problems.