Double integrals over general areas
Connecting area and volume views
Or...connecting "area between curves" and "volume of a solid" interpretations of double-integrals.
Consider the green area in the $xy$ plane
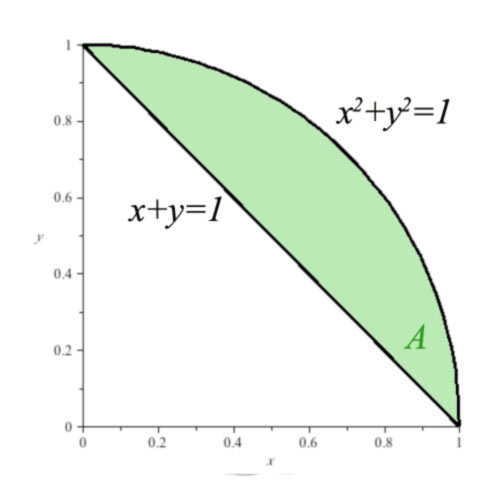
According to the "area between curves" view, the area in green is given by: $$\begineq A &=& \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}} dA\\ &=&\int_{x=0}^{1}\left(\int_{y=1-x}^{\sqrt{1-x^2}} \,dy\right)\,dx\\ &=&\int_{x=0}^{1}\left(\left. y\right|_{y=1-x}^{\sqrt{1-x^2}}\right)\,dx\\ &=&\int_{x=0}^{1}\left(\sqrt{1-x^2}-(1-x)\right) \,dx\\ &=&\frac{\pi}{4} -\frac 12 \endeq $$
But we could instead think about that double integral as the volume above a non-rectangular area in the $xy$ plane, going up to the surface $f(x,y)=1$, like this... $$\begineq V &=& \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}} dA\\ &=& \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}} 1\,dA\\ &=& \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}} f(x,y)\,dA\\ \endeq$$
Then the volume corresponds to this solid:
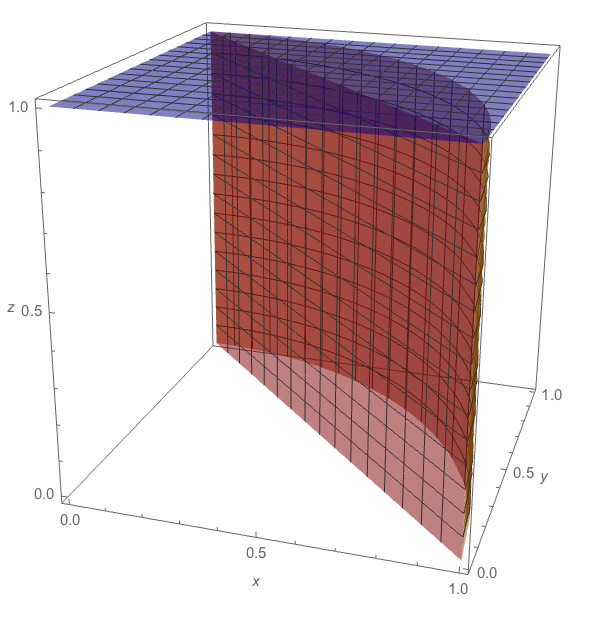
- The base in the $xy$ plane is the green area $A$,
- it extends straight up from $A$,
- to a height of $1$...
- that is, it is bounded above by the surface $f(x,y)=1$.
The value of the volume integral: $$ V = \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}} 1 \,dy\,dz$$ is the same as the value of the area between curves that we first considered.
Double integrals above general areas
$$\iint_A f(x,y)\,dA=?$$ Let's generalize our interpretation of this integral as the volume under $f(x,y)=1$ to *any* function $f(x,y)$: In general this double integral is...
- The volume of a solid,
- bounded, on the bottom, by a non-rectangular area, $A$, in the $xy$ plane.
- going straight up from that area,
- bounded above by a surface $f(x,y)$
This volume integral is represented in the picture below:
$$V = \int_{x=0}^{1}\int_{y=1-x}^{\sqrt{1-x^2}}
x\,dA$$
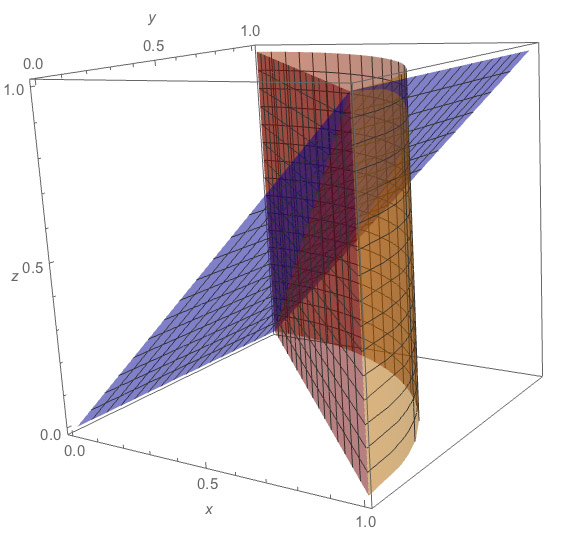
It's bounded by $f(x,y)=x$ above.
- See this Mathematica notebook (12.3)
We shall find that now, the order of integration *does* affect how we write down the limits of a double integral.
Order matters.
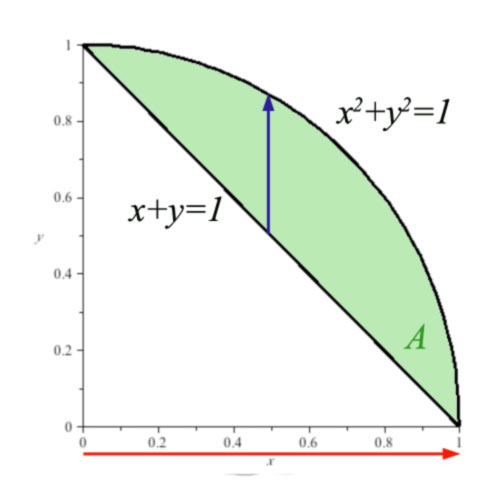 $\iint_A f(x,y)\,dA$
$\iint_A f(x,y)\,dA$
- Integrate first with respect to y
- This gives us the area, $A(x)$, of a slice through the solid above the blue arrow, which depends on $x$, $$A(x)=\int_{y=1-x}^{\sqrt{1-x^2}} f(x,y)\,dy.$$
- Integrate second with respect to x
Written... $$\int_{x=0}^1A(x)\,dx=\int_{x=0}^1\int_{y=1-x}^{\sqrt{1-x^2}} f(x,y)\,dy\,dx$$
Order matters..
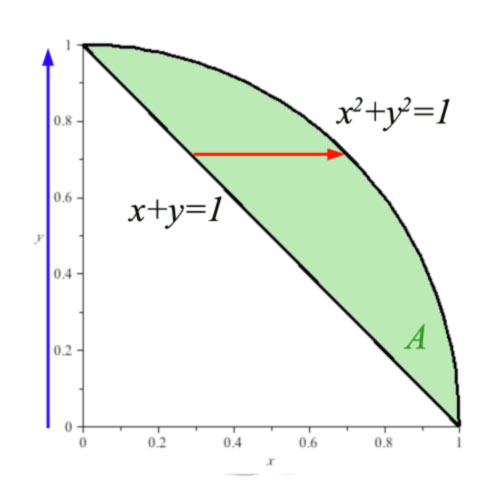 $\iint_A f(x,y)\,dA$
$\iint_A f(x,y)\,dA$
- Integrate first with respect to x,
- This gives us the area, $A(y)$, of a slice through the solid above the red arrow, which depends on $y$, $$A(y)=\int_{x=1-y}^{\sqrt{1-y^2}} f(x,y)\,dx$$
- Integrate second with respect to y
Written... $$\int_{y=0}^1A(y)\,dy=\int_{y=0}^1\int_{x=1-y}^{\sqrt{1-y^2}} f(x,y)\,dx\,dy.$$
Example
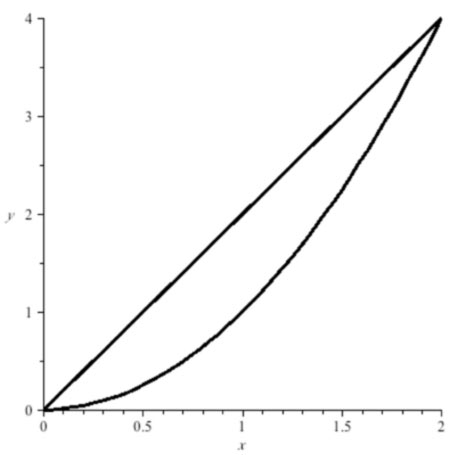 $\iint_A (4x+2)\,dA$
$\iint_A (4x+2)\,dA$
Regions
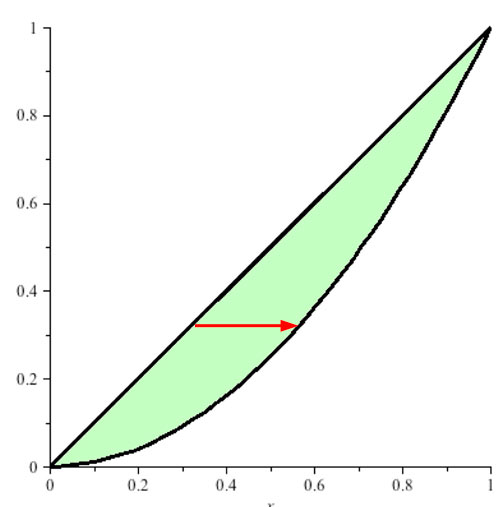
You should be able to sketch the region of integration in $x$ and $y$ given a double integral. For example: $$\int_0^1\int_y^\sqrt{y} x^2y^2\,dx\,dy$$
...means $$\int_{y=0}^1\left(\int_{x=y}^\sqrt{y} x^2y^2\,dx\right)\,dy$$
$\Rightarrow$
Changing the order of integration
$$\int_{x=-1}^0\int_{y=0}^{x+1}e^{x+y}dy\,dx+\int_{x=0}^1\int_{y=0}^{1-x} e^{x+y}dy\,dx$$
$\Rightarrow$
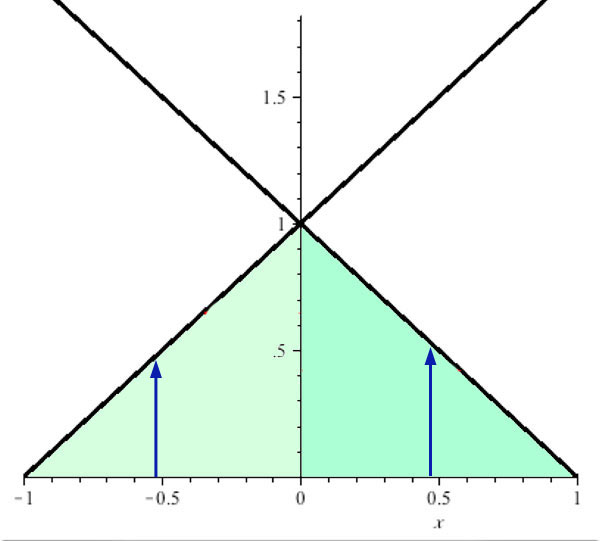
We could get the same result in one integral, integrating first over $x$ then $y$ like this...
The line $y=x+1$ can be re-arranged to $x=y-1$.
The line $y=1-x$ can be re-arranged to $x=1-y$:
$$\int_{y=0}^1\int_{x=y-1}^{1-y} e^{x+y}dx\,dy$$
To do
- Double Integrals Practice: #5-7
- Limits on Double Integrals
- Double Integrals: Problems