Polar integrals [12.4]

Kakslauttanen Igloo Village, Finland
Area in Cartesian coordinates
In Cartesian coordinates...
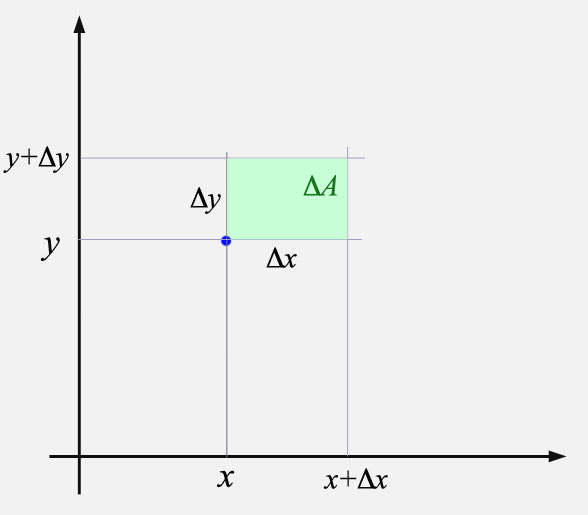
As $\Delta x \to dx$ and $\Delta y\to dy$, the rectangle has an area which approaches $$dA=dx\,dy$$
Area in Polar coordinates
In polar coordinates...
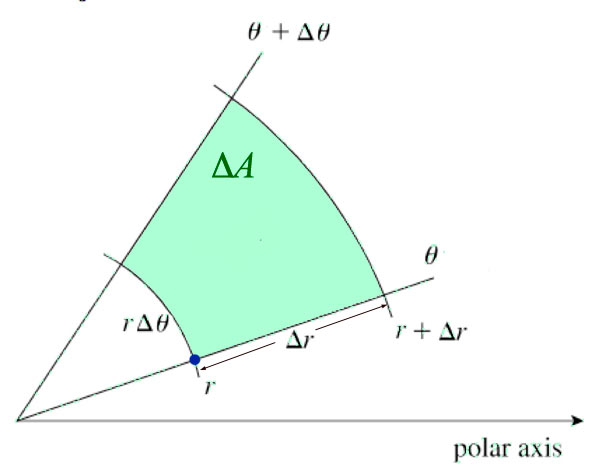
As $\Delta \theta \to d\theta$ and $\Delta r\to dr$, the shaded region becomes more nearly rectangular, with sides of length $r\,d\theta$ and $dr$, so... $$dA=r\,d\theta\,dr=r\,dr\,d\theta.$$
Area of a circle
The area of a circle of radius $R$ can be found by this double integral: $$\begineq A &=&\iint_A dA =\int_{\theta=0}^{2\pi}\int_{r=0}^R r\,dr\,d\theta \\ &=&\int_{\theta=0}^{2\pi}\left( \left. \frac{r^2}{2} \right|_0^R\right)\,d\theta\\ &=&\frac{R^2}{2}\int_{\theta=0}^{2\pi}d\theta=\frac{R^2}{2}2\pi = \pi R^2. \endeq $$
Double polar integrals.
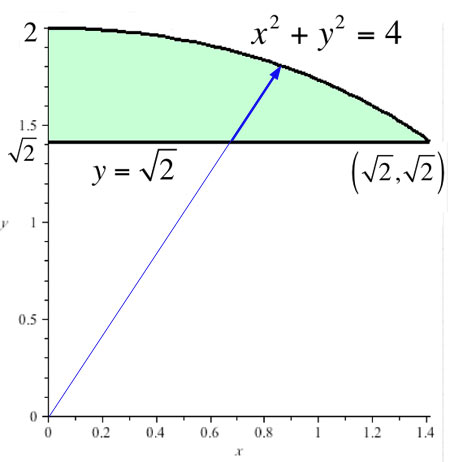
$A=\iint_A f(r,\theta)\,dA=?$
Double polar integrals..
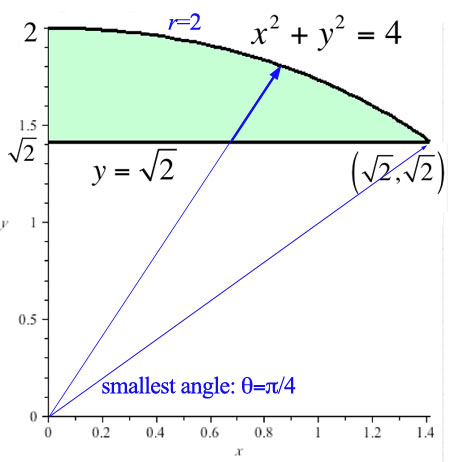
$A=\iint_A f(r,\theta)\,dA=?$
The line $\sqrt 2=y=r\sin\theta$ becomes
$r(\theta)=\frac{\sqrt 2}{\sin\theta}=\sqrt 2 \csc\theta$.
The double integral becomes: $$A=\int_{\theta=\pi/4}^{\pi/2} \int_{r=\sqrt 2\csc\theta}^2 f(r,\theta)\,r\,dr\,d\theta.$$
Converting...
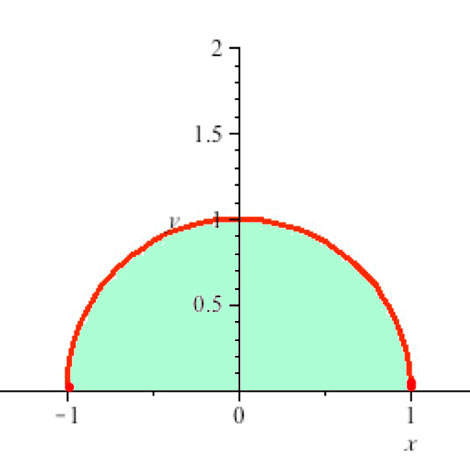
Converting a double-integral in Cartesian coordinates to polar coordinates:
$\iint_A e^{x^2+y^2}dA=\int_{x=-1}^1\int_{y=0}^{\sqrt{1-x^2}}e^{x^2+y^2}dy\,dx=...$
- $r$ runs from 0 to 1.
- $\theta$ runs from 0 to $\pi$.
- ah, $x^2+y^2=r^2$
- $dx\,dy=dA=r\,dr\,d\theta$
$$\begineq\iint_Ae^{r^2}dA &=&\int_{\theta=0}^{\pi}\int_{r=0}^1e^{r^2}r\,dr\,d\theta\\ &=&\int_{\theta=0}^{\pi}\left(\left.\frac{e^{r^2}}{2}\right|_{r=0}^1\right)\,d\theta\\ &=& \left(\frac{e-1}{2}\right)\int_{\theta=0}^{\pi}\,d\theta = (e-1)\frac\pi 2 \approx 2.70 \endeq $$
ToDo
Double integrals in polar coordinates