Parametric surfaces [12.6]

Review Parametric Surfaces [10.5]...

• As parameters $u$ and $v$ are varied in some domain $D$,
• The vector $\myv r(u,v)=\langle\,x(u,v),\,y(u,y),\,z(u,v)\rangle$ traces out a surface $S$ in 3D.

  Tangent plane approximation

  Outline of the tangent plane approximation:
  

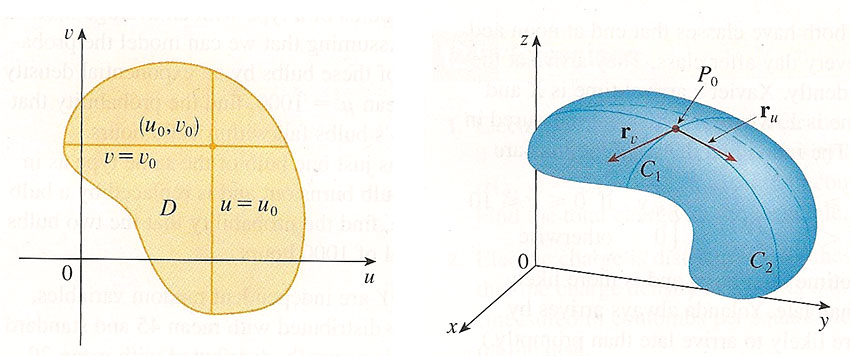
  • As $v$ varies in $D$, ($u$ is constant), $\myv r$ traces the curve $C_1$. A tangent vector to $C_1$ is $$\myv r_v =\langle \frac{\del x}{\del v}, \frac{\del y}{\del v},\frac{\del z}{\del v} \rangle\equiv \langle x_v, y_v, z_v \rangle.$$ [What does that subscript mean in this context??]
  • As $u$ varies in $D$, ($v$ is constant), $\myv r$ traces the curve $C_2$. A tangent vector to $C_2$ is $$\myv r_u=\langle x_u, y_u, z_u \rangle$$
  • Increasing $v$ to $v+\Delta v$ in $D$ leads to a change of $\myv r$ on the surface of approximately $\Delta v\, \myv r_v$.
  • Increasing $u$ to $u+\Delta u$ in $D$ leads to a change of $\myv r$ on the surface of approximately $\Delta u\, \myv r_u$.
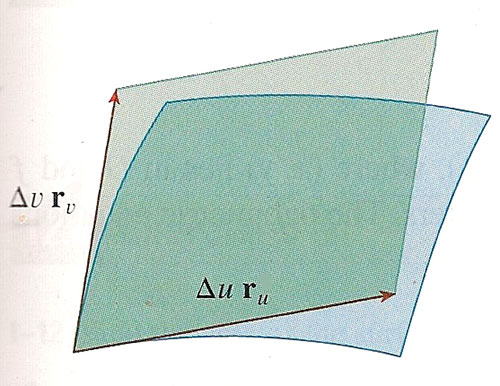  • The area of the parallelogram shown is
    
    $|(\Delta v\,\myv r_v)\times(\Delta u\,\myv r_u)|$
      =$|\myv r_v\times\myv r_u|\Delta A$
    
    Where $\Delta u \Delta v=\Delta A$, an area in $D$.
  • This cross product is approximately equal to $\Delta S$, the area of a "patch" of the surface.

  In the limit $\Delta u\to du,\ \Delta v \to du$, the approximation gets more exact, and the surface area of $S$ is $$S=\iint_D dS = \iint_D |\myv r_u\times \myv r_v|\,dA.$$

  [Later on, we'll consider surface integrals [13.6]. It will be useful that the direction of the cross-product $\myv r_u \times \myv r_v$ is perpendicular to (normal to) the surface.]

  Surface area of a graph defined in terms of $(x,y)$

  For the special case of the surface $z=f(x,y)$, $u\to x$, $v\to y$, such that $(x,y)$ is in the domain $D$, the surface area can be written (see *below) : $$S=\iint_D\sqrt{1+\left(\frac{\del z}{\del x}\right)^2 + \left(\frac{\del z}{\del y}\right)^2 } \, dA $$

  Example

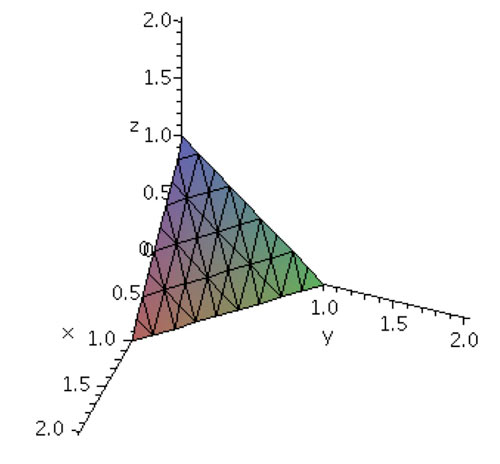  Area of the surface shown of the plane:
  $z=1-x-y$

  $$\begineq S&=&\iint_D\sqrt{1+\left(\frac{\del z}{\del x}\right)^2 + \left(\frac{\del z}{\del y}\right)^2 } \, dA \\ &=&\iint_D\sqrt{1+\left(-1\right)^2 + \left(-1\right)^2 } \, dA =\iint_D\sqrt{3} \, dA \\ &=&\sqrt 3 \iint_D dA=\sqrt 3 A_D=\sqrt 3 *(1*1)/2=\sqrt 3/2 \endeq $$

  Check the result by using geometry to calculate the surface area...

  Surface area of a graph defined in terms of $(x,y)$

  The general expression for surface area: $$S=\iint_D dS = \iint_D |\myv r_u\times \myv r_v|\,dA.$$

  For the special case of the surface $z=f(x,y)$, $u\to x$, $v\to y$, such that $(x,y)$ is in the domain $D$, $$\begineq \myv r_u\to \myv r_x &=&\langle \frac{\del x}{\del x}, \frac{\del y}{\del x},\frac{\del z}{\del x} \rangle\\ &=&\langle 1, 0,\frac{\del z}{\del x} \rangle\\ \endeq$$ Since $x$ and $y$ are at right angles (orthogonal), a change in $x$ does not change $y$, and vice versa. So $\frac{\del x}{\del y}= \frac{\del y}{\del x}=0$.
  
  And, $$\begineq \myv r_v\to \myv r_y &=&\langle 0, 1,\frac{\del z}{\del y} \rangle\\ \endeq$$

  Writing out the cross product of the two vectors: $$\begineq \myv r_x \times \myv r_y &=& \text{det}\begincv \hat i&\hat j& \hat k\\ 1&0&\frac{\del z}{\del x }\\ 0&1&\frac{\del z}{\del y } \endcv \\ &=& -\frac{\del z}{\del x }\hat i-\frac{\del z}{\del y }\hat j +\hat k. \endeq$$

  And therefore the surface area can be written as: $$A_S=\iint_D|\myv r_x\times \myv r_y|\,dA = \iint_D \sqrt{1+\left(\frac{\del z}{\del x}\right)^2 + \left(\frac{\del z}{\del y}\right)^2 } \, dA $$