Surface integrals

For example: how much water is flowing out through a surface?
Parameterizing surfaces
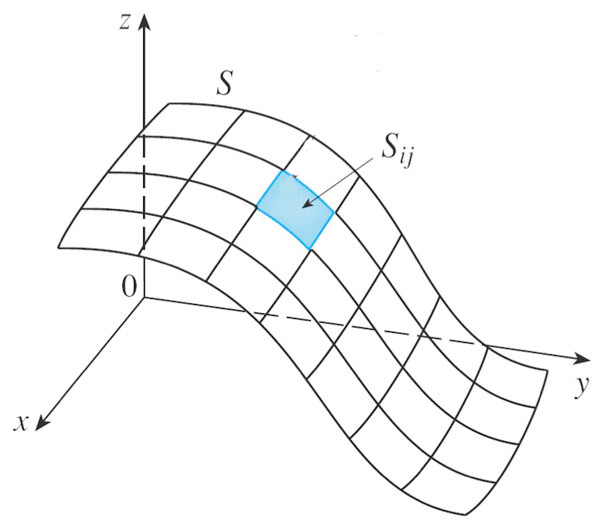
In the topic on parametric surfaces [12.6]
we saw how to express a surface $S$ in terms of two parameters $u$ and $v$ in a domain $D$.
The surface is specified by a mapping
$$\myv r=x(u,v)\uv i+y(u,v)\uv j+z(u,v)\uv k$$
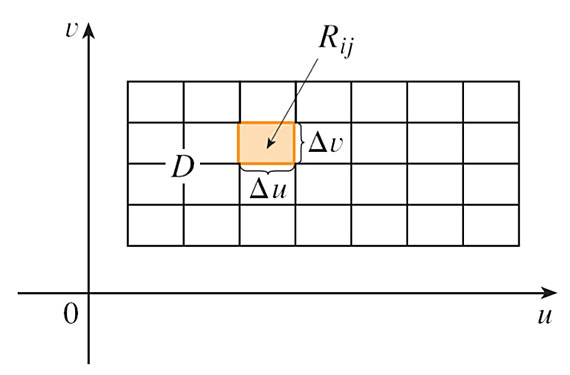
The surface area is $$A_S=\iint_S 1\,dS = \iint_D\left|\myv r_u \times \myv r_v \right|\,dA.$$ where $$\myv r_u \equiv \langle \frac{\del x}{\del u}, \frac{\del y}{\del u},\frac{\del z}{\del u} \rangle\equiv \langle x_u, y_u, z_u \rangle,$$ and similarly for $\myv r_v$.
The surface integral
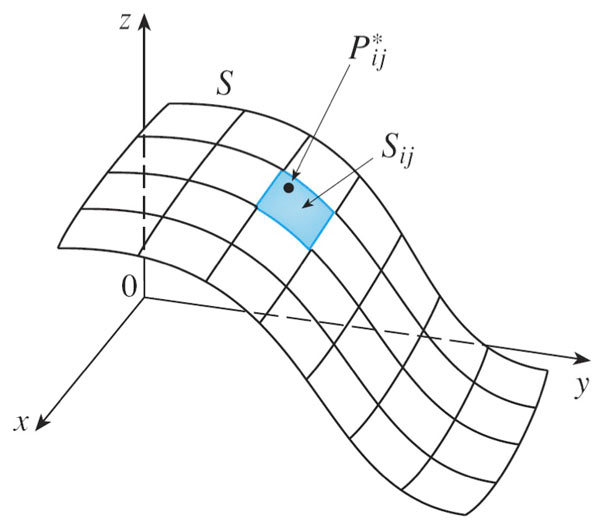
Defining the surface integral in terms of the Riemann sum
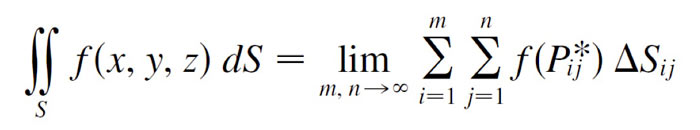
General definition of a surface integral if the surface $x=x(u,v)$, $y=y(u,v)$ and $z=z(u,v)$ is parameterized in the parameter space $u$, $v$:
$$\iint_S f(x,y,z)\,dS= \iint_D f(\myv r(u,v)) \left|\myv r_u \times \myv r_v \right|\,du\,dv.$$
But we can define a surface in terms of $x=x$, $y=y$, and $z=g(x,y)$. That is, $x$ and $y$ are the two 'parameters'. Then the definition of a surface integral is:
$$\iint_S f(x,y,z)\,dS= \iint_D f(x,y,g(x,y))\sqrt{1 + \left(\frac{\del g}{\del x}\right)^2 +\left(\frac{\del g}{\del y}\right)^2 }\,dx\,dy.$$
Oriented surface
We'll shortly be integrating normal components of vector fields.
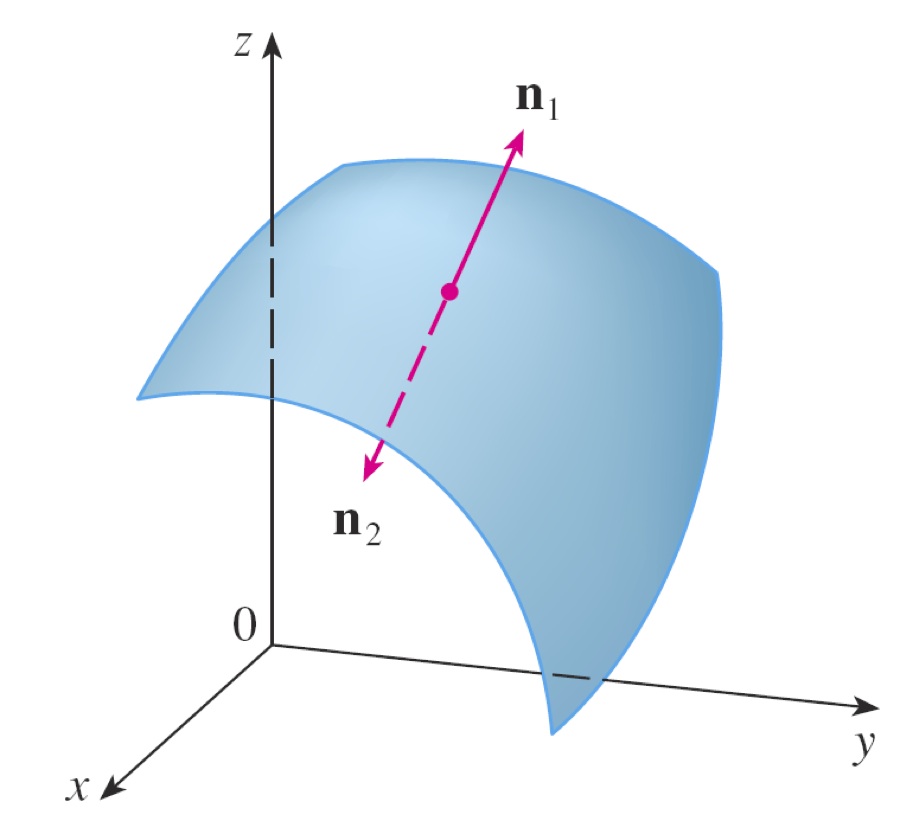 There are two possible surface normal orientations.
There are two possible surface normal orientations.
For closed surfaces we can define a convention for which surface normal to choose.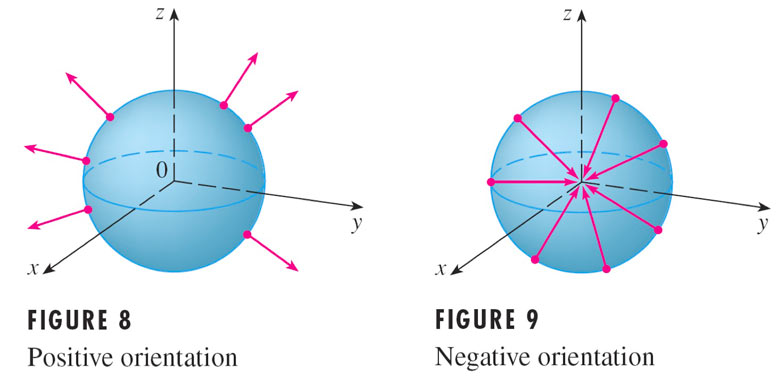
Surface, or flux integral
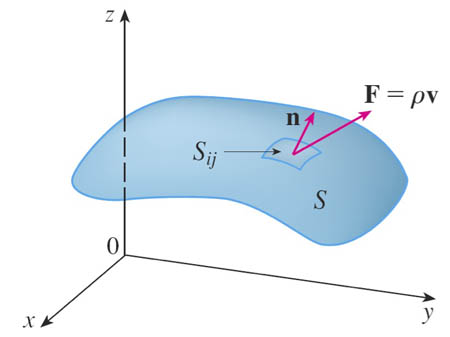 If necessary, we will use a simpler convention that the positive normal direction is up.
If necessary, we will use a simpler convention that the positive normal direction is up.
The flux integral or the surface integral of the normal component of a vector field is $$\iint_S\myv F\cdot \uv n \,dS$$
In terms of the parameters $u$ and $v$, note that $\myv r_u \times \myv r_v$ is normal to the surface. Therefore,
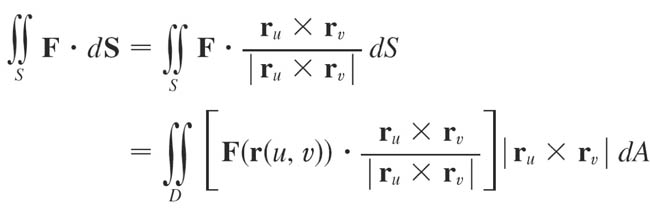
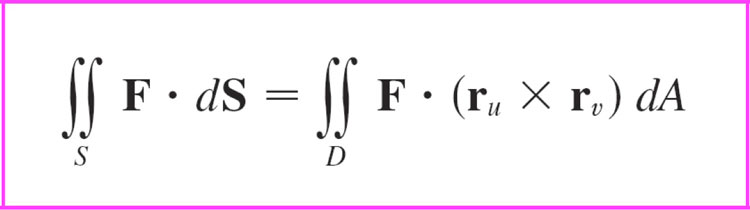
Example-really ought to have one
To do
Let $\myv F(x,y,z)=x^2\uv i$. Find $\iint_S\myv F\cdot d\myv S$ where $S$ is the surface of a box with one vertex at the origin, and extending 1 unit in the positive $\uv i$, $\uv j$, and $\uv k$ directions. $d\myv S$ points in the direction normal to the surface.
First sketch the box. Then find $d\myv S$ for each of the six faces. (For example, for the top face, it is $d\myv S=\uv k\,dA=\uv k\,dx\,dy$.) Then calculate the double integral for each face. (It's easier than it sounds!)
See 13.6.surf.nb