Surface integrals
For example: how much water is flowing out through a surface?
Parameterizing surfaces
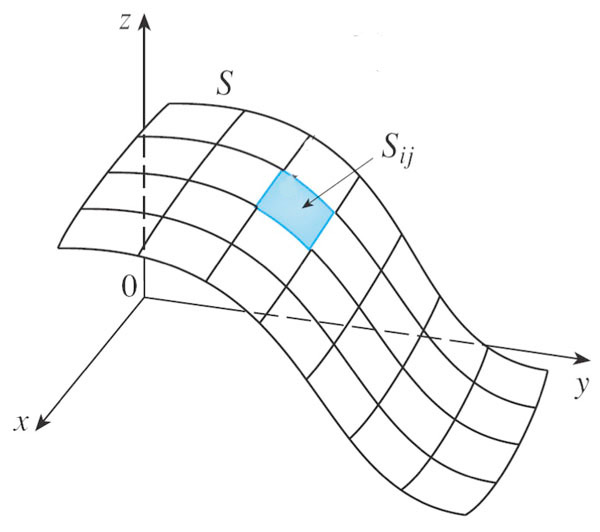
In the topic on parametric surfaces [12.6]
we saw how to express a surface $S$ in terms of two parameters $u$ and $v$ in a domain $D$.
The surface is specified by a mapping
$$\myv r=x(u,v)\uv i+y(u,v)\uv j+z(u,v)\uv k$$
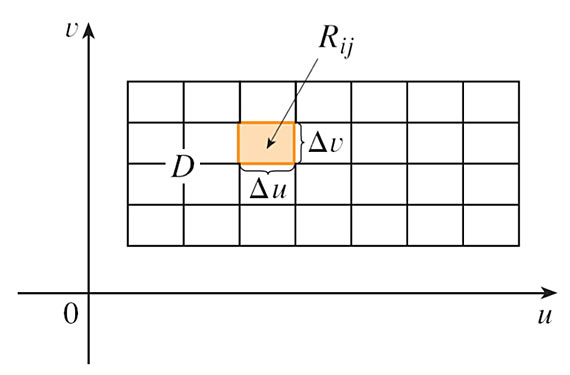
The surface area is $$A_S=\iint_S 1\,dS = \iint_D\left|\myv r_u \times \myv r_v \right|\,dA.$$ where $$\myv r_u \equiv \langle \frac{\del x}{\del u}, \frac{\del y}{\del u},\frac{\del z}{\del u} \rangle\equiv \langle x_u, y_u, z_u \rangle,$$ and similarly for $\myv r_v$.
The surface integral
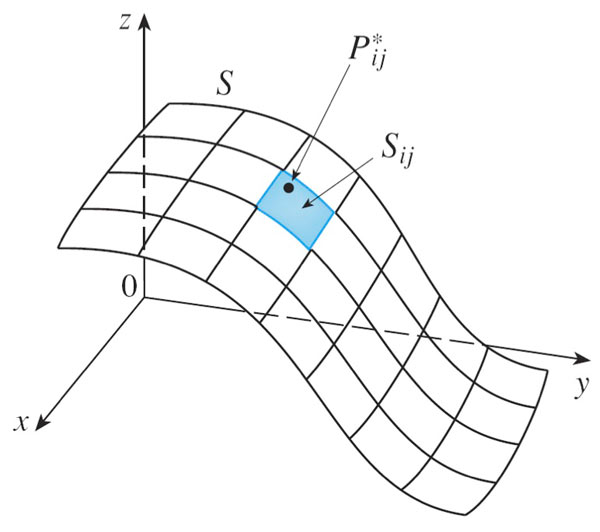
Defining the surface integral in terms of the Riemann sum
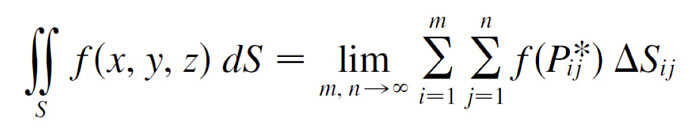
General definition of a surface integral if the surface $x=x(u,v)$, $y=y(u,v)$ and $z=z(u,v)$ is parameterized in the parameter space $u$, $v$:
$$\iint_S f(x,y,z)\,dS= \iint_D f(\myv r(u,v)) \left|\myv r_u \times \myv r_v \right|\,du\,dv.$$
But we can define a surface in terms of $x=x$, $y=y$, and $z=g(x,y)$. That is, $x$ and $y$ are the two 'parameters'. Then the definition of a surface integral is:
$$\iint_S f(x,y,z)\,dS= \iint_D f(x,y,g(x,y))\sqrt{1 + \left(\frac{\del g}{\del x}\right)^2 +\left(\frac{\del g}{\del y}\right)^2 }\,dx\,dy.$$
Oriented surface
We'll shortly be integrating normal components of vector fields.
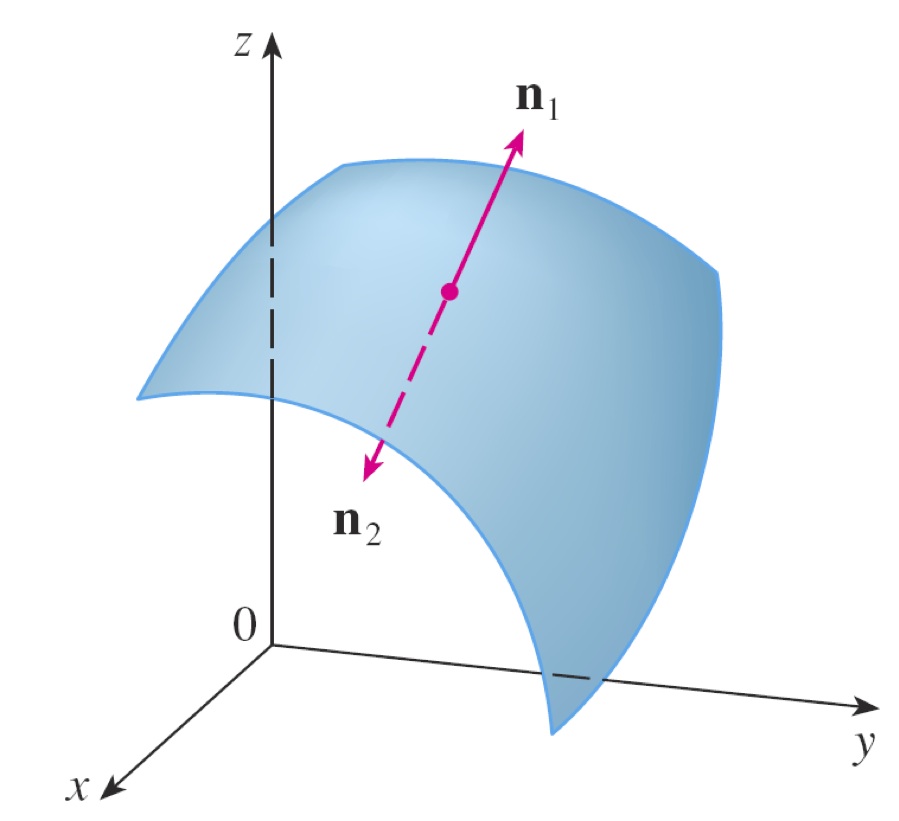There are two possible surface normal orientations.
For closed surfaces we can define a convention for which surface normal to choose.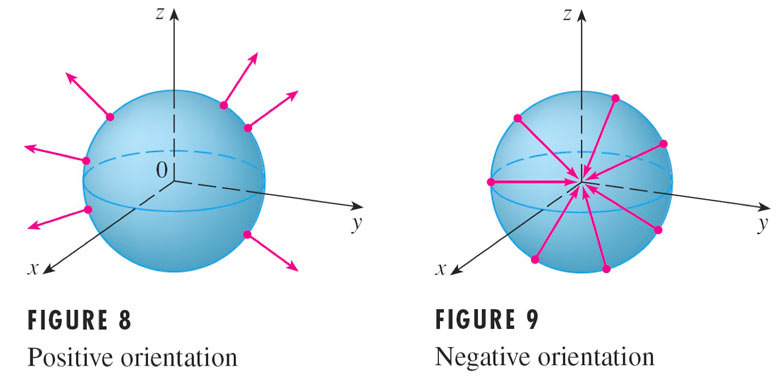
Surface, or flux integral
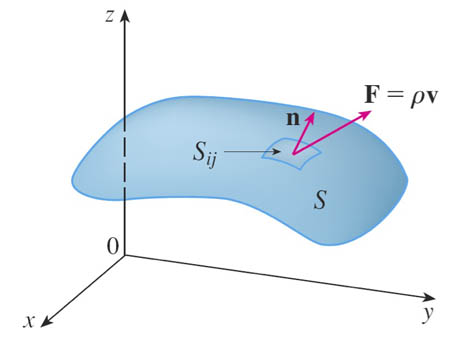If necessary, we will use a simpler convention that the positive normal direction is up.
The flux integral or the surface integral of the normal component of a vector field is $$\iint_S\myv F\cdot \uv n \,dS$$
In terms of the parameters $u$ and $v$, note that $\myv r_u \times \myv r_v$ is normal to the surface. Therefore,
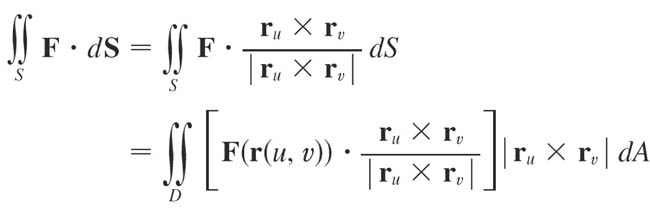
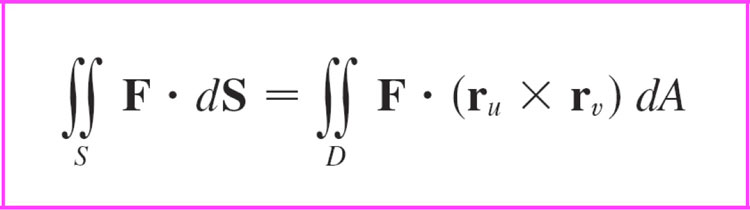
Example-really ought to have one
To do
Let $\myv F(x,y,z)=x^2\uv i$. Find $\iint_S\myv F\cdot d\myv S$ where $S$ is the surface of a box with one vertex at the origin, and extending 1 unit in the positive $\uv i$, $\uv j$, and $\uv k$ directions. $d\myv S$ points in the direction normal to the surface.
First sketch the box. Then find $d\myv S$ for each of the six faces. (For example, for the top face, it is $d\myv S=\uv k\,dA=\uv k\,dx\,dy$.) Then calculate the double integral for each face. (It's easier than it sounds!)
See 13.6.surf.nb