Change of variables [12.9] - Transformations

Change of variables: 1D
Consider the difficult-looking integral... $$\int_{x=0}^3 x \cos(x^2-3)\,dx.$$
Do a change in variables to $u=x^2-3$. What to do about $dx$?: $$\frac{du}{dx}=2x\ \ \Rightarrow \ \ du=2x\,dx.$$
And now we can re-write the integral as $$\begineq\int_{x=0}^3 x \cos(x^2-3)\,dx&=& \int_0^3 \frac 12 \cos(x^2-3)\,2x\,dx\\ &=&\int_{u(0)=-3}^{u(3)=6} \frac 12 \cos(u)\,du=\frac 12\left(\sin(6)-\sin(3)\right). \endeq$$
That is, treating $u= u(x)$ as a function of $x$... $$\int_a^b f(u(x))u'(x)\,dx=\int_{u(a)}^{u(b)}f(u)\,du$$
But we will be interested in the situation where $x=x(u)$, so I will re-write this, interchanging $x$ and $u$, as... $$ \int_{x(a)}^{x(b)}f(x)\,dx = \int_a^b f(x(u))\frac{dx}{du}\,du.$$
This change of variables can be thought of as a change of coordinate systems.
That derivative $\frac{dx}{du}$ is playing the role of a "conversion factor" for lengths when you switch between $u$- and $x$-coordinates.
Example: Linear transformations in 2-d
Let's assume that we can make a linear transformation between 2 2-d coordinate systems, $(x,y)$ and $(u,v)$: $$x(u)=au+bv+c$$ $$y(u)=du+ev+f$$
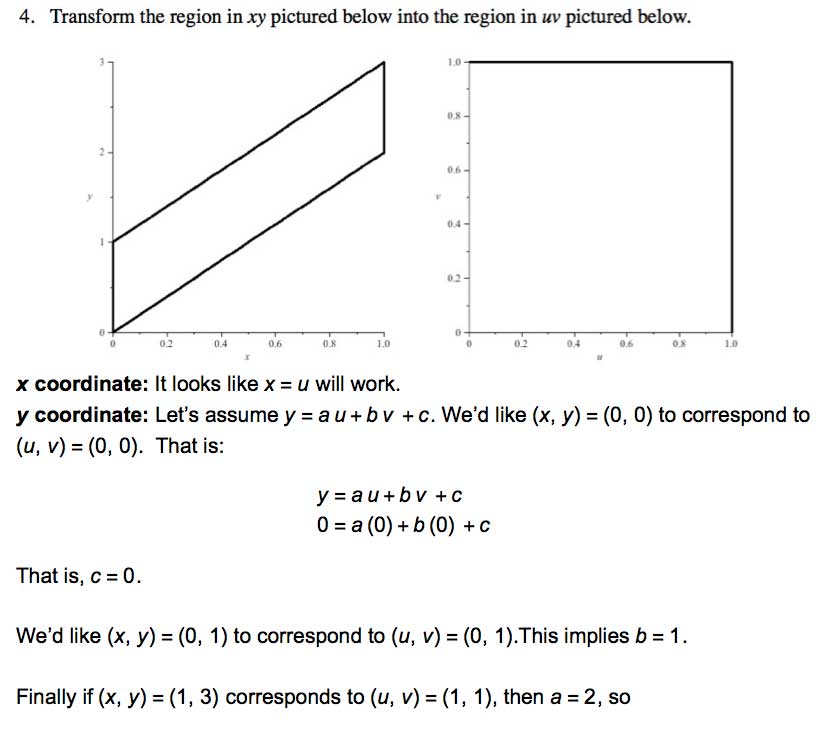
We know how to convert an integral from Cartesian to a handful of other coordinate systems.
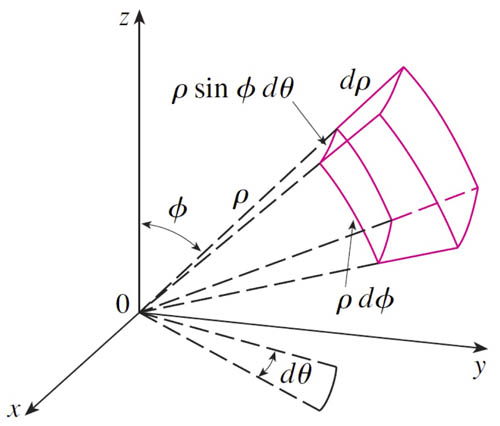
for example, $\to$ spherical coordinates:
$$\iiint_E f(x,y,z)\,dx\,dy\,dz = \iiint_E f(\rho,\theta,\phi) \rho^2 \sin \phi \,d\rho\,d\theta\,d\phi.$$
Our goal is to come up with a general way to convert double or triple integrals from one system $(x,y,z)$ to another system $(u,v,w)$ given only the coordinate transformation rules $x(u,v,w)$, $y(u,v,w)$, and $z(u,v,w)$.
We shall see that something called the Jacobian plays the role of conversion factor.
General Transformations
Transformations [Powerpoint format]
- Transformations handout.
- Change of variables handout.
Putting all the derivations together, an integral in terms of $x$ and $y$ can be carried out in terms of coordinates $u$ and $v$ instead like this...
