Characterizing vector fields
*Some* vector fields, $\myv F$, represent the gradient of a function, $\myv F=\myv \grad f$.
In the next few class sessions we'll be trying to figure out:
- How to tell if a vector field is the gradient of a function,
- How to find the function $f$, given $\myv F$.
- How this makes some line integrals *a lot* easier to evaluate.
Gradients
The gradient of a scalar field is a vector field. $$ \myv \grad f(x,y)=f_x(x,y)\uv i+f_y(x,y)\uv j=\myv v(x,y)$$
$$\myv \grad f(x,y,z)=f_x(x,y,z)\uv i+f_y(x,y,z)\uv j+f_z(x,y,z)\uv k=\myv v(x,y,z)$$
Gradient Fields
Some (but not all) vector fields are gradient fields. Consider $f(x,y)=x^2+xy+y^2$. The gradient is $$\myv \grad f=\langle f_x,f_y \rangle = (2x+y)\uv i+ (2y+x)\uv j.$$
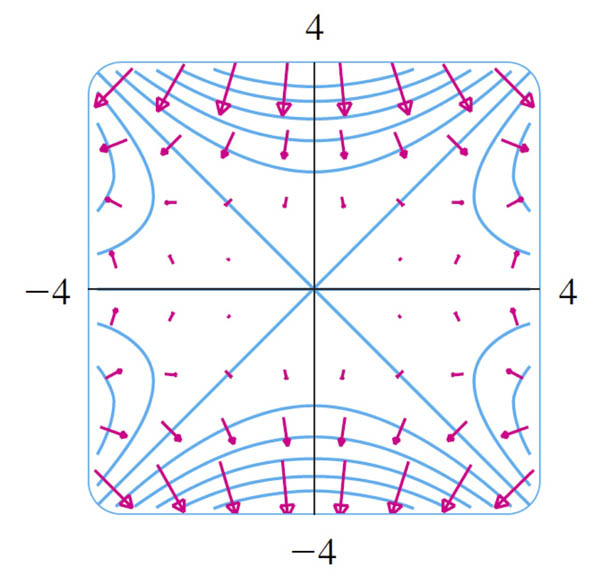
Graphing the function $f$ below in contour plot. What can you say about
- The direction of the vectors in the vector field $\myv v=\myv \grad f$?
- Where are the vectors representing $\myv v$ longer or shorter?
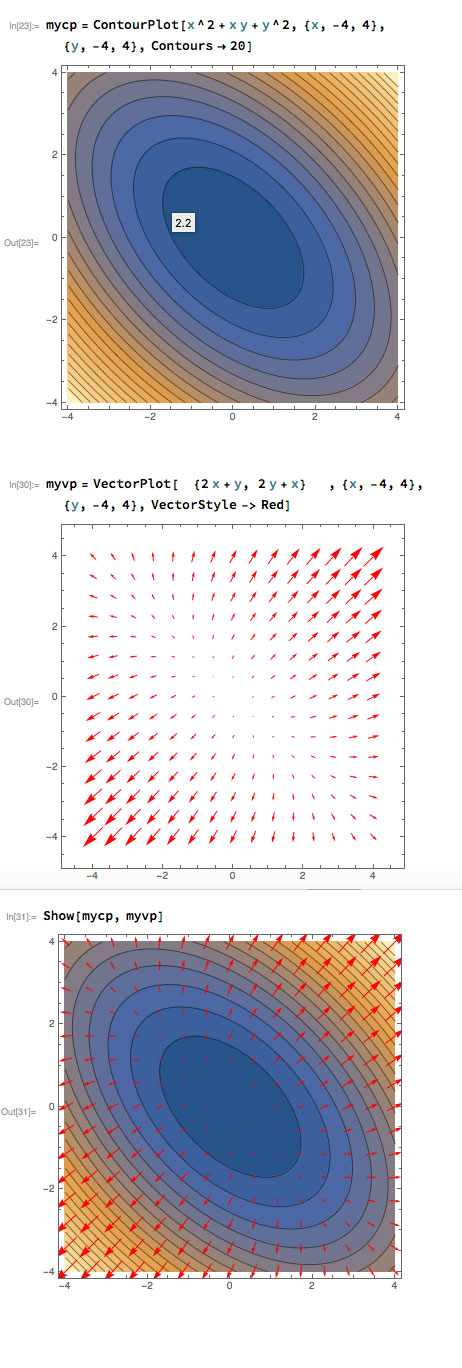
Grad / Contour example
Grad / Contour example
Grad / Contour example
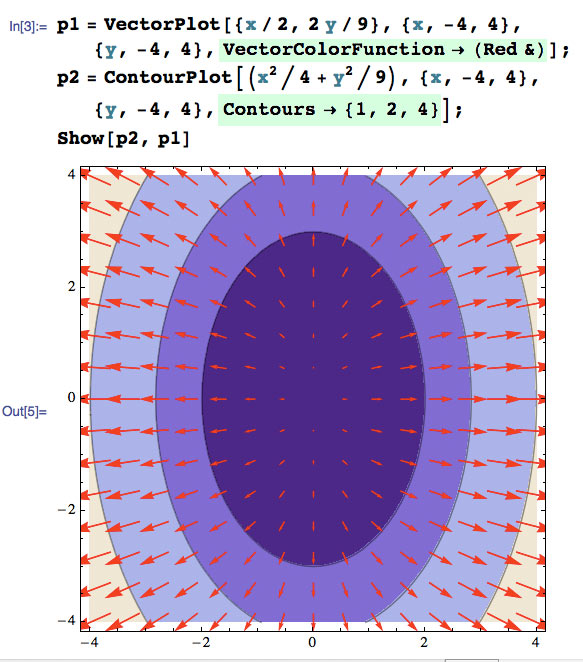
In Mathematica
Plotting contours and gradient vector fields together...
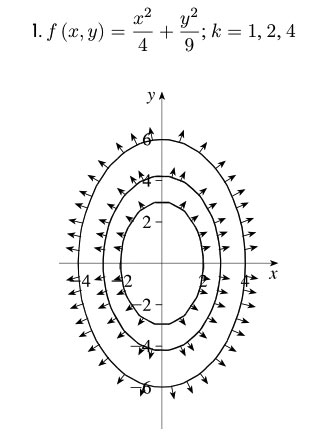
$$f(x,y)=\frac{x^2}{4}+\frac{y^2}{9}$$
Contours for $f=1,2,9$.
You'll try a couple of these in the lab...
- $f(x,y)=xy-2x$
- $f(x,y)=\sin(x)+\sin(y)$
- $f(x,y)=\sin(x+y)$
Conservative fields
Consider the vector field... $$\myv F(x,y)=2x\uv i+y\uv j$$
Can you find--or actually, just guess--a function $f(x,y)$ such that $$\myv F(x,y) = \myv \grad f(x,y)?$$
If such a function $f$ exists:
- $f(x,y)$ is called a potential function for the vector field $\myv F$.
- $\myv F(x,y)$ is a conservative vector field.