[9.2] - Reading Assignment
Read section 9.2 in the textbook. Make sure you have a sense of the following terms and concepts (shown here for 2-dimensional vectors):
[${}^*$ - means some part of this terminology may not be in the textbook]
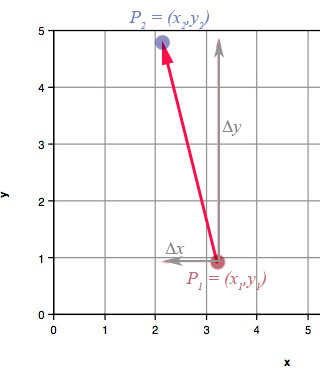
In the diagram above...
- $P_1$ is the initial point (tail) and $P_2$ is the terminal point (head)
- The components of the vector $\myv{P_1P_2}$ are $$\langle \Delta x, \Delta y \rangle\equiv \langle x_2-x_1, y_2-y_1 \rangle.$$
- ${}^*$ Standard position means "tail at the origin". The "position vector of a point" $B$ is a vector in standard position with its tip at $B$.
- ${}^*$ Length of a vector $\equiv$ magnitude $\equiv$ "measure" $\equiv$ "norm"
- Two vectors, $\myv a$ and $\myv b$ are equivalent or equal if they have the same length and the same direction.
- A unit vector always has a length of 1. A unit vector parallel to $\myv u$and pointing in the same directions is $\uv u = \myv u / |\myv u|$.
[9.2] Reading questions
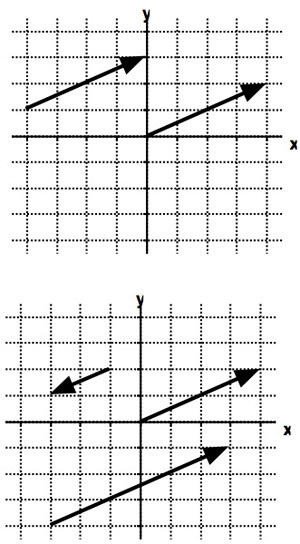 For the 2 vectors in the top diagram, which statements are true? (Can be more than one.)
For the 2 vectors in the top diagram, which statements are true? (Can be more than one.)- They have the same direction.
- They have the same length.
- They are parallel to each other.
- They are equivalent vectors.
- For the 3 vectors in the bottom diagram, which statements are true?
- They have the same direction.
- They have the same length.
- They are parallel to each other.
- They are equivalent vectors.
- Sketch on the bottom diagram a unit vector which points in the same direction as the longest vector of the 3 shown.
- On the bottom diagram, indicate which of the vectors is a "position vector" for the point $(-3,1)$.
- If $\myv a=\langle a_1,a_2,a_3 \rangle$ has $a_2 \gt 0$ and $a_3\lt 0$, then is the $z$-component of $-3\myv a$ positive or negative?
- What's one or two "muddy points" in the reading that you'd like to clear up. Or (if nothing seemed muddy) one thing that you *wonder* about.