[9.2] - Reading Assignment

Read section 9.2 in the textbook. Make sure you have a sense of the following terms and concepts (shown here for 2-dimensional vectors):
[${}^*$ - means some part of this terminology may not be in the textbook]

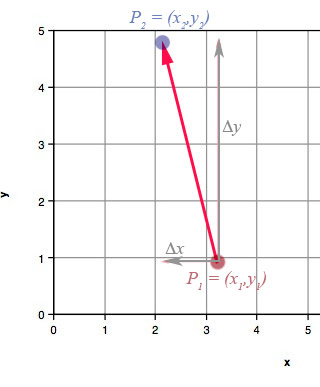
In the diagram above...

• $P_1$ is the initial point (tail) and $P_2$ is the terminal point (head)
• The components of the vector $\myv{P_1P_2}$ are $$\langle \Delta x, \Delta y \rangle\equiv \langle x_2-x_1, y_2-y_1 \rangle.$$
• ${}^*$ Standard position means "tail at the origin". The "position vector of a point" $B$ is a vector in standard position with its tip at $B$.
• ${}^*$ Length of a vector $\equiv$ magnitude $\equiv$ "measure" $\equiv$ "norm"
• Two vectors, $\myv a$ and $\myv b$ are equivalent or equal if they have the same length and the same direction.
• A unit vector always has a length of 1. A unit vector parallel to $\myv u$and pointing in the same directions is $\uv u = \myv u / |\myv u|$.

[9.2] Reading questions

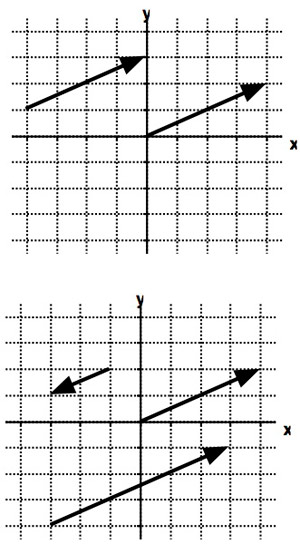1. For the 2 vectors in the top diagram, which statements are true? (Can be more than one.)
   1. They have the same direction.
   2. They have the same length.
   3. They are parallel to each other.
   4. They are equivalent vectors.
2. For the 3 vectors in the bottom diagram, which statements are true?
   1. They have the same direction.
   2. They have the same length.
   3. They are parallel to each other.
   4. They are equivalent vectors.
3. Sketch on the bottom diagram a unit vector which points in the same direction as the longest vector of the 3 shown.
4. On the bottom diagram, indicate which of the vectors is a "position vector" for the point $(-3,1)$.
5. If $\myv a=\langle a_1,a_2,a_3 \rangle$ has $a_2 \gt 0$ and $a_3\lt 0$, then is the $z$-component of $-3\myv a$ positive or negative?
6. What's one or two "muddy points" in the reading that you'd like to clear up. Or (if nothing seemed muddy) one thing that you *wonder* about.