[12.7] - Triple integrals / Volume
- Find the volume of the figures shown below, using both a triple integral, and geometry.


-
Sketch the solid whose volume is given by
$$\int_0^4\int_0^{\frac{4-x}{2}} \int_0^{\frac{12-3x-6y}{4}} dz\,dy\,dx$$
Then rewrite the integral in the order $\int \int \int dy\,dx\,dz$ with the appropriate limits of integration.
-
Find the volume of the tetrahedron bounded by the coordinate plane
$z=4-4x-2y$.

-
Find the volume of the tetrahedron shown below.
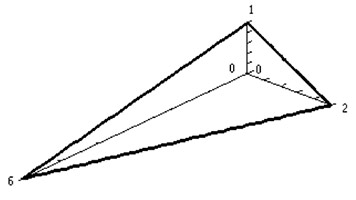
- First figure, by geometry $V=\frac12*(2\times1\times1)=1$;
Setting up the integral... $$\int_{x=0}^2\int_{y=0}^1\int_{z=0}^{1-y} dz\,dy\,dx=\int_{x=0}^2\int_{y=0}^1(1-y) \,dy\,dx=...$$ - By geometry $V=4\times2\times2+4\times2\times\frac124=32$
- $$\begineq V&=&\iiint dV=\iiint dx\,dy\,dz\\ &=& \int_{x=0}^1\int_0^{y=2-2x}\int_0^{z=4-4x-2y}dz\,dy\,dx\\ &=&\frac43 \endeq $$