Motion of a charge in a magnetic field
- The Lorentz force acts on charges which are moving in a magnetic field. $$\myv{F} = q \myv{v} \times \myv{B}.$$
- The magnetic force on a charged particle is another kind of velocity dependent force.
- Results in spiraling motion about field lines.
- A compact, useful way to represent circular motion is to use Euler's law to represent complex numbers as vectors in 2-d polar coordinates (woo and hoo!)
- Earth possesses a strong magnetic field $\Rightarrow$ thick atmosphere (unlike Mars) and $\Rightarrow$ abundant life-as-we-know-it (unlike Mars).
Lorentz force
The Lorentz force acting on a particle with charge
$q$ in a uniform magnetic field $\myv{B}$ (which we'll take to be pointing up in the $\uv
z$ direction) is
$$\myv{F} = q \myv{v} \times \myv{B}.$$
Equation of motion
$$\begineq m \dot{\myv{v}} &=& q \myv{v} \times \myv{B}= q \det \begincv \uv{x}&\uv{y}&\uv{z}\\v_x&v_y&v_z\\0&0&B_z\endcv \\ &=&q v_y B_z \uv{x} - q v_x B_z \uv{y}\endeq $$
Review vector cross products if you need to!
Separating out the components in Cartesian coordinates and calling $B_z = B$ we get three equations: $$m \dot{v}_x = qBv_y;\ m \dot{v}_y = -qBv_x;\ m \dot{v}_z = 0.$$
Divide them all by $m$: $$ \dot{v}_x = \frac{qB}{m}v_y;\ \dot{v}_y = -\frac{qB}{m}v_x;\ \dot{v}_z = 0.$$
The solution to this last one is $z(t) = z_0 + v_{z0} t$: So, the $z$-coordinate of the particle is changing with a constant speed.
From coupled 1st order DEs to a single 2nd order DE
[To solve numerically the "skateboard on a half-pipe", we went from one 2nd order DiffEq to two couple first order ones. Now we'll go the other way!]
We can take the time derivative of that first equation, $$\ddot v_x =\frac{qB}{m}\dot{v}_y,$$ and then use the second equation to substitute in for $\dot{v}_y$ in terms of $v_x$, leaving $$ \ddot{v}_x = - \left(\frac{qB}{m}\right)^2 v_x.$$
This is a second-order differential equation for $v_x$, and it looks like it would have sine or cosine solutions...for example $v_x=A\sin\left[\frac{qB}{m}t\right]$.
But instead, let's return to those two coupled equations and use complex numbers instead...
The Complex plane & Euler's Formula
Read over this brief and historical justification of Euler's formula. (Your textbook also connects the series expansion of $e^{i\theta}$ with the series for sine and cosine functions.)
$$e^{i\phi}=\cos\phi+i\sin\phi.$$
This material on Taylor series (mathphys) shows how to get the series approximation of $\sin x$ by Taylor-expanding the sine function about zero: $$\sin(x)=x -x^3/3!+x^5/5!-x^7/7!+x^9/9!-....$$ and visualizing how the series approaches $\sin x$.
Perhaps you'll recall that you can represent a complex number as a vector in 2 dimensional space where the real portion is the $x$-component and the imaginary part is the $y$-component of the vector. Here we have a depiction of the complex number $-2 + 4i$: The blue dot has Cartesian components $(x,y)=(-2,4)$.
The position vector with components $(-2,4)$ is also shown on there as the blue arrow.
We can talk about a vector in terms of its length and direction. This is the way that a vector is described in polar coordinates: This position vector:
- has a length of $r=\sqrt{x^2+y^2}=\sqrt{(-2)^2+(4)^2}=\sqrt{20}\approx 4.47$,
- makes an angle (taking into account which quadrant it's in) of $\phi=\pi - \arctan(y/x)=\pi-\arctan(-4/2)=$ 2.03 radians ($\approx$ 117${}^o$) with the positive $x$ axis.
Euler's formula is $e^{i \phi } = \cos \phi + i \sin \phi$. More generally, we can write this as $re^{i \phi } = r\cos \phi + i r\sin \phi$ where the real and imaginary components of a complex number are connected to $r$ and $\phi$ in the formula like the $x$ and $y$ coordinates are connected through a conversion to polar coordinates $r$ and $\phi$.
So, apparently $-2+4i = 4.47e^{i 2.035}$ are equivalent ways of writing the same complex number.
1.) Sketch the complex number $\xi=3-4i$ in the complex plane. Then using cartesian$\to$polar conversions, write $\xi$ in the form $r\,e^{i\phi}$, where $r$ and $\phi$ themselves are real numbers.
$$r=\sqrt{3^2+(-4)^2}=5;\ \ \phi=arctan(-4/3)=-0.927$$ and therefore: $$3-4i=5e^{-i 0.927}.$$ Your calculator will tell you that -0.927 radians is -53${}^o$. And your sketch of the point (3, -4) should tell you that the vector is in the fourth quadrant.
2.) Sketch the complex number $\xi=5e^{i\frac{13\pi}{4}}$ in the complex plane. Then using polar$\to$cartesian conversions, write $\xi$ in the form $X+Yi$, where $X$ and $Y$ are real numbers.
A vector of length 5. The (counterclockwise) angle of rotation, $\phi=\frac{13}{4}\pi=(1+\frac 58)2\pi$ indicates that we must make 1 full rotation, and then 5/8 more of a rotation from the $x$-axis, so the vector is in quadrant III, pointing 45 degrees below the $-x$ direction. $$X=5*cos[13\pi/4]=-3.54; \ \ Y=5*sin[13\pi/4]=-3.54$$ so $$5e^{i\frac{13\pi}{4}}=-3.54 -3.54i.$$ From the right triangle, you can perhap also see that, since $X^2=Y^2$, we'd have $2X^2=25\Rightarrow |X|=\sqrt{25/2}=3.54$.
3.) Consider the function $\xi(t)=e^{i4t}$. In the complex plan, this describes a position vector of a constant length, 1. And its tip traces out a circle as time progresses. Draw the trajectory of the tip of the vector. Indicate where on the circle the tip of the vector is at $t=0$. Figure out how much time it takes for the tip of the circle to return to its starting point. (This is the period, "$T$".) Also figure out whether the tip is rotating clockwise or counterclockwise around the origin.
$\xi$ is equal to 1 times the imaginary exponential. So the tip of the vector describes a circle of radius one.
At $t=0$, $\xi(0)=e^{i0}=1$. So, the vector is pointing at $X+iY=1+i0$, 1 on the real ($x$) axis.
When the angle in $e^i\phi$ increases to $2\pi$, one rotation is complete, and the vector is pointing in the $x-direction again. This will happen after a time $T$ fulfilling:
$$4T=2\pi\Rightarrow T=\pi/2.$$
The tip rotates counterclockwise. You can graph out a couple angles to see...
4.) Consider the function $\xi(t)=4e^{i\pi/6}e^{-i2t}$. In the complex plan, sketch out the circular trajectory that the tip of the position vector $\xi(t)$ traces out with time. What is its radius? Indicate where on the circle the tip of the vector is at $t=0$. Figure out how much time it takes for the tip of the circle to return to its starting point. (This is the period, "$T$".) Also figure out whether the tip is rotating clockwise or counterclockwise.
A position vector in the complex plane traces out a circle of radius 4. It starts pointing 30${}^0$ ($\pi/6$ radians) above the $x$ axis, and moves clockwise. When $2T=2\pi\Rightarrow T=\pi$ seconds have passed, the vector will have completed one whole rotation since $t=0$.
5.) Using the same $\xi(t)$ defined in the last problem: Carry out the multiplication of the two exponentials, so that you can express the the function in terms of just one $e$ raised to a more complicated-looking power. Now use Euler's formula to write $\xi(t)$ as $X(t)+iY(t)$, where $X(t)$ is the real portion of this function and $Y(t)$, the imaginary portion of this function.
$$\xi(t)=4e^{-i2t+i\pi/6}=4e^{-i(2t-\pi/6)}=4\cos(-(2t-\pi/6))+4i\sin(-(2t-\pi/6)) .$$
Equations of motion in complex form
Defining this constant $\omega$--called the cyclotron frequency $$\omega = \frac{qB}{m},$$
[We shall see that the period for the motion to repeat will be $2\pi/\omega$. Since there are $2\pi$ radians in a circle, I prefer to think of $\omega$ as having units of "Radians"/sec. But technically, radians (the ratio of an arclength to a radius) are unitless, so traditionally $\omega$ is said to have units of 1/s.]
We can rewrite the equations of motion in the $x$- and $y$-directions as: $$\dot{v}_x = \omega v_y ;\ \dot{v}_y = -\omega v_x.$$
Using Euler's formula, we can think of the $x$- and $y$-components as real and imaginary parts of a complex number. '$\eta$' (The lower and upper case 'eta's are $\eta$ and $H$, pronounced in modern Greek as "ay" like 'play'): $$\eta \equiv v_x + v_y i,$$ and then our two equations of motion can be re-written as one differential equation for a complex variable ('2-d vector in the complex plane'), $\eta$: $$\begineq\color{red}{\dot{\eta}}\color{black} =& \dot{v}_x + i \dot{v}_y \\ =& \omega v_y - i \omega v_x\\ =& -i \omega (v_x + i v_y) &= \color{red}{-i \omega \eta}. \endeq$$
Solution for the velocity
The equation of motion is now $$\dot{\eta} = -i \omega \eta$$
And so the solution is $\eta = A e^{-i \omega t}$.
$e^{-i \omega t}$ is a unit-length vector rotating around (clockwise? counterclockwise?) with period $2\pi/\omega$. And so multiplying this unit length rotating vector by the complex $A$ makes it look like $A$ is the radius of circular motion. But wait there's more...
Let's have $A$ be a constant which is complex as well. We can write it as $A = a e^{i \delta}$ where $a$ and $\delta$ are real numbers. $a$, is the amplitude (radius) of the circular rotation of the complex quantity representing $v_x$ and $v_y$. And now $\delta$ is useful as the "phase angle" specifying the angular offset at $t=0$. We could also say that $a$ is the maximum value of either $v_x$ or $v_y$, which is just $v$.
Solution for the position
$\eta(t)$ is the complex representation of the velocity. To get (a complex representation of) the position we need to integrate the velocity, along the lines of $\int_{x_0}^{x(t)} \,dx = \int_{0}^{t} v(t)\,dt$.
So let's use a different complex variable $\xi$ for the position. (Xi pronounced 'xsee', upper/lower $\Xi$/$\xi$ as in... TA$\Xi$I, of course) as: $\xi(t) \equiv x(t) + iy(t)$: $$\begineq \int_{\xi(0)}^{\xi(t)} d\xi' &=& \int_0^{t}\eta(t')\,dt' = \int_0^{t} ae^{i \delta} e^{-i\omega t'}dt' \\ &=& \frac{i}{\omega}ae^{i\delta}e^{-i\omega t} = \frac{e^{i\pi/2}}{\omega} \eta(t)=\frac{1}{\omega}ae^{i(\delta+\frac\pi2)}e^{-i\omega t} \\ \xi(t) - \xi(0)&=& \frac{e^{i\pi/2}}{\omega} \eta(t)\endeq$$
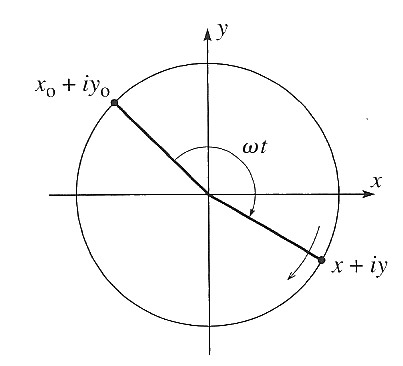This looks like circular motion:
- starting at $\xi(0) = x_0 + i y_0$,
- rotating with angular speed $\omega$ (period $= 2\pi/\omega$)
- in a circle of radius $a/\omega = v / \omega = \frac{mv}{qB}=\frac{p}{qB}$
- the velocity has a phase offset of $\pi/2$ relative to the position--A fancy way of saying that the velocity is at right angles to the position.
Motion along field lines
Charged particles spiral around field lines...as seen here.
And this may be the reason there is a lot of life on Earth, but nothing discernable on Mars.
What? How?...
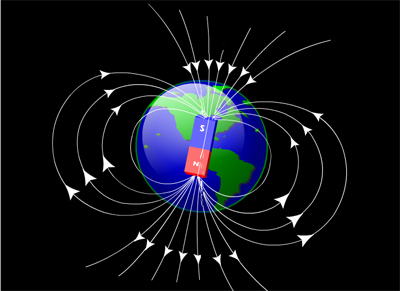
Earth has a strong magnetic field, as if there were a strong magnet at Earth's center (or some sort of current rotating around its axis), with its S pole lined up very nearly along the direction of the North Pole.
This strong magnetic field causes charged particles from the "solar wind" (protons, electrons, ions...) to follow field lines that run into Earth's surface near the North and South Poles.
But the "piling" up of charged particles creates a shock wave that directs most of the solar wind harmlessly beyond Earth.
This is a good thing, because these solar wind particles possess kinetic energy in excess of what is needed to break the molecular bonds of typical gases such as $O_2$, $CO_2$.
The average "temperature" of an atmosphere is proportional to the average kinetic energy ($\frac 12mv^2$) of molecules in the atmosphere. If you think about it, this means that small, single atoms with the average kinetic energy (as a result of collisions with other molecules in the atmosphere) are moving much faster than bigger molecules.
In fact, some fraction of the single atoms in the outer stretches of the atmosphere are likely to have velocities in excess of the "escape velocity" needed to make it out of the planetary "gravitational well".
With Mars' much weaker magnetic field, the solar wind has likely been breaking Mars' atmosphere's heavier molecules into smaller pieces since the planet's dynamo "slowed down", more than 4 billion years ago. This has caused the atmosphere to dissipate into space, to the point that atmospheric pressure on Mars is less than 1% of atmospheric pressure on Earth.
Homework
2.46, 2.47, 2.55 (a & b only)