Green's Theorem [13.4]
Window at Cambridge University honoring George Green
Another fundamental theorem relates
- a double integral of partial derivatives over an area to,
- a line integral around the border of the region.
Line integrals and areas
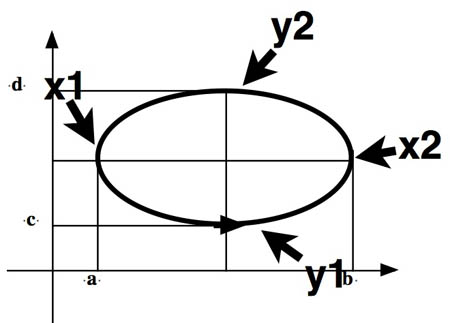
Let $A$ be the area inside the closed curve.
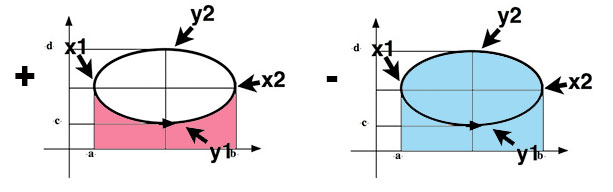
$$\begineq \int_C y\,dx&=&\int_{x=a}^by_1(x)\,dx+\int_b^ay_2(x)\,dx\\
&=&\int_{x=a}^by_1(x)\,dx\color{blue}{-}\int_a^b y_2(x)\,dx=-A\endeq
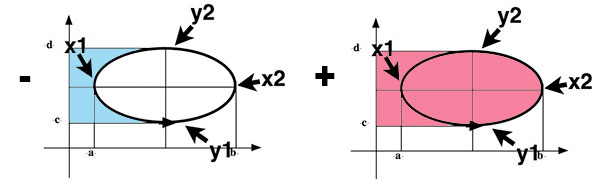
$$
$$\begineq \int_Cx\,dy&=&\int_{x=d}^cx_1(y)\,dx+\int_c^dx_2(y)\,dx\\
&=&-\int_{x=c}^dx_1(y)\,dx+\int_c^dx_2(y)\,dx=A\endeq$$
$\Rightarrow \oint_{\circlearrowleft C} x\,dy-y\,dx =2A$
No detailed knowledge of the exact path, $C$, was used in this derivation.
Consider $$\myv F=-y \uv i + x\uv j\equiv P\uv i + Q\uv j$$ We can write the integral above as $$\oint_{\circlearrowleft C } \myv F \cdot d\myv r = \oint_{\circlearrowleft C } P\,dx + Q\,dy= \oint_{\circlearrowleft C }x\,dy-y\,dx =2A$$
Now it just so happens that this double integral over the region $D$ bounded by $C$ gives the same result $$\begineq \iint_D \left( \frac{\del Q}{\del x}- \frac{\del P}{\del y} \right) \,dx\,dy &=& \iint_D \left( \frac{\del x}{\del x}- \frac{\del (-y)}{\del y} \right) \,dx\,dy \\ &=&\iint_D \left( 1+1 \right) \,dx\,dy = 2A \endeq $$ ...also without detailed knowledge of $C$ (*).
This is a special case of
Green's Theorem
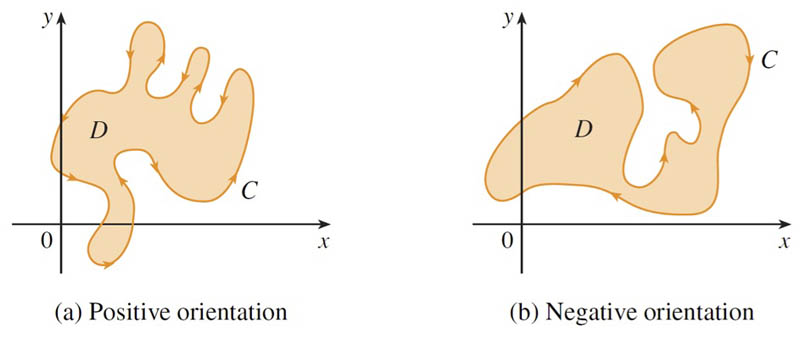
Positive oriention - $\circlearrowleft$ - interior points on the left as $C$ is traversed.
[From this point on, I'll omit the $\circlearrowleft$. You should assume, unless it's stated otherwise, that $\oint$ means $\oint_\circlearrowleft$.]
Application - Area
Apparently the area of any simple, connected region can be calculated from any of these line integrals: $$A= \oint x\,dy = -\oint y\,dx =\frac 12\left(\oint x\,dy -\oint y\,dx\right).$$
Example-Testing Green's theorem
$$\oint_C(P\,dx +Q\,dy) =\iint_D\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\,dA$$
Let $P=xy$ and $Q=-y^2$. Calculate both ways:
$$\oint xy\,dx - y^2\,dy \equiv \oint P\,dx + Q\,dy.$$
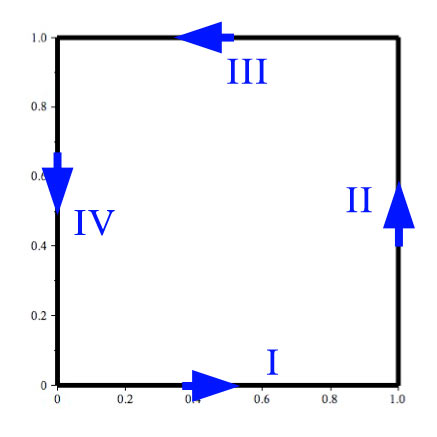
on this path.
Calculating the line integral
- $y=0$ and $dy=0$. $$\int_I P\,dx= \int_{0}^1 x*0\,dx = 0$$
- $x=1$ and $dx=0$. $$\int_{II} Q\,dy= \int_{0}^1 -(y^2)\,dy = -\frac 13$$
- $y=1$ and $dy=0$. $$\int_{III} P\,dx= \int_{1}^0 (x*1)\,dx =-\frac 12$$
- $x=0$ and $dx=0$. $$\int_{IV} Q\,dy= \int_{1}^0 -(y^2)\,dy =-\left.\frac{y^3}{3}\right|_1^0=+\frac 13 $$
$$I+II+III+IV=0-\frac 13 -\frac 12 +\frac 13=-\frac 12.$$
As a double integral
$\myv F=P\uv i+Q\uv j$
$P=xy \Rightarrow \frac{\del P}{\del y}=x.$
$Q=-y^2 \Rightarrow \frac{\del Q}{\del x}=0.$
$$\begineq \iint_D\left( \frac{\del Q}{\del x} -\frac{\del P}{\del y}\right)dA &=&\int_{y=0}^1\int_{x=0}^1 \left(0-x\right)\,dx\,dy\\ &=&-\frac{1}{2}\int_{y=0}^1\,dy=-\frac 12.\\ \endeq $$
Example
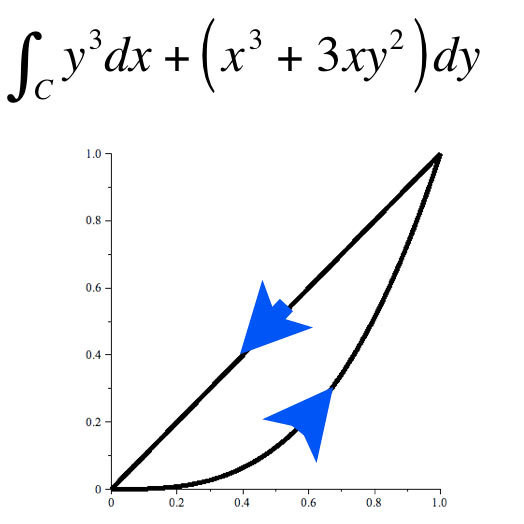Compute the line integral around the boundary by converting to a double integral over the area.
$P=y^3 \Rightarrow \frac{\del P}{\del y}=3y^2.$
$Q=x^3+3xy^2 \Rightarrow \frac{\del Q}{\del x}=3x^2+3y^2.$
Green's theorem says that the line integral around the boundary (positive sense) is equal to... $$\begineq \oint_CP\,dx+Q\,dy &=& \iint_D\left( \frac{\del Q}{\del x} -\frac{\del P}{\del y}\right)dA =\iint_D\left( 3x^2+3y^2-(3y^2) \right)dA\\ &=&\iint_D 3x^2 dA=\int_{x=0}^1\int_{y=x^2}^x 3x^2\,dy\,dx \endeq $$
To do
- Green's Theorem problems
Two Vector forms of Green's theorem
There are two implications of Green's theorem in terms of vector integrals. One involves the curl and one involves the divergence.
Tangential component of a vector field
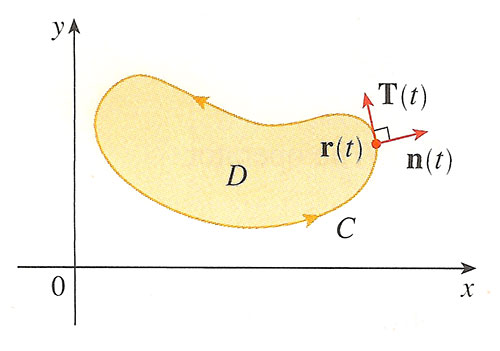We have already seen that the left hand side of Green's theorem is the integral of the tangential component of $\myv F$ around $C$, that is, with $\myv F=P\uv i + Q\uv j$,
$$\oint P\,dx+Q\,dy=\oint \myv F\cdot d\myv r = \oint \myv F\cdot \uv T\,ds$$
where
$$\uv T=\frac{\myv r'(t)}{|\myv r'(t)|}
= \frac{x'(t)}{|\myv r'(t)| }\uv i + \frac{y'(t)}{|\myv r'(t)| }\uv j.$$
The right-hand side of the Green's theorem $$r.h.s. = \iint_D\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\,dA$$ can be expressed in terms of a curl:
Treating $\myv F$ as a three-dimensionsal field with a $z$-component of zero... $$\myv \grad \times \myv F=\text{det} \begincv \uv i &\uv j&\uv k \\ \frac{\del}{\del x} & \frac{\del}{\del y} & \frac{\del}{\del z}\\ P & Q & 0 \endcv = \left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\uv k. $$ So, Green's theorem in terms of the curl of $\myv F$ is...
$$\oint_C \myv F\cdot \uv T\,ds = \iint_D \myv \grad \times \myv F \cdot \uv k\,dA. $$
The integral of the tangential component along the boundary is called the circulation.
In terms of fluid flow, this relates the integral of the curl of a vector field over a domain, $D$ to the circulation on the boundary.
[Fundamental theorem: relates a differential of a vector function to the value of the vector function on the boundary.]
Generalizing to 3-dimensions
$$\oint_C \myv F\cdot \uv T\,ds = \iint_S \myv \grad \times \myv F \cdot d\myv S $$
- $d\myv S=\uv n\,dS$,
- $\uv n$ is the local normal unit vector to a 3-dimensional surface, \
- $dS$ is the differential of surface area, and
- The path, $C$, is a curve in space which is the boundary of the surface $S$.
Go to 13.7 - Stokes' theorem.
Normal component of a vector field
The unit tangent vector was: $$\uv T=\frac{\myv r'(t)}{|\myv r'(t)|} = \frac{x'(t)}{|\myv r'(t)| }\uv i + \frac{y'(t)}{|\myv r'(t)| }\uv j.$$
The normal vector, $\uv n$, will be at right angles to $\uv T$, and lies in the $x$-$y$-plane. There are two choices. The outward normal vector has components:
$$\uv n = = \frac{y'(t)}{|\myv r'(t)| }\uv i - \frac{x'(t)}{|\myv r'(t)| }\uv j.$$
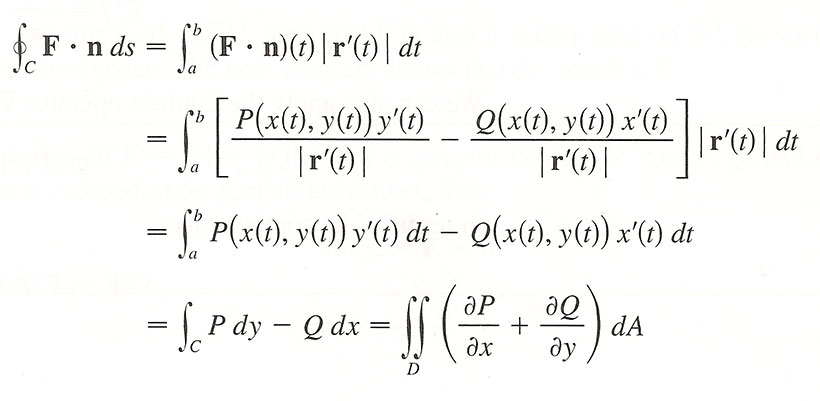
The quantity on the right in $(...)$ is the divergence of $\myv F$, so...
$$\oint_C \myv F\cdot \uv n\,ds = \iint_D \myv \grad \cdot \myv F \,dA. $$
The integral of the normal component over the boundary is called the flux
In terms of an incompressible fluid, this says that the integral of the divergence (all the faucets minus the drains) in $D$ is equal to the fluid flux (amount of fluid per second) flowing out of the region.
Generalizing to 3 dimensions
$$\oiint_S\myv F\cdot d\myv S=\iiint_E \myv \grad \cdot \myv F\,dV $$
- The ∯ symbol means a surface integral over a closed surface.
- $d\myv S=\uv n\,dS$ is a vector differential which is everywhere normal to the surface $S$.
- $S$ is the boundary of a 3-d solid, $E$.
Go to 13.8 - the divergence theorem